Question

Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ${\omega _0}$ and has rotational kinetic energy ${K_0}$. The top disc is initially at rest. It then falls and sticks to the bottom disc. The change in the rotational kinetic energy of the system is
A. $\dfrac{{{K_0}}}{2}$
B. $ - \dfrac{{{K_0}}}{2}$
C. $ - \dfrac{{{K_0}}}{4}$
D. $\dfrac{{{K_0}}}{4}$

Answer 1

Hint: In this question we have to use the law of conservation of angular momentum to find the new angular velocity when the discs are attached. Then by comparing the kinetic energy of the discs before and after the attachment of top disc to bottom disc we will find the change in rotational kinetic energy.

Complete step by step answer:
Rotational kinetic energy of a particle is defined as the energy associated with the particle when it is in circular motion. The velocity acquired by a particle due to its rotation or revolution is known as angular velocity.

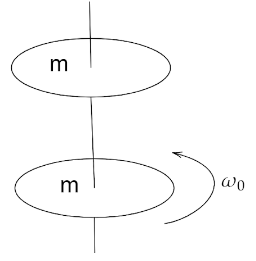
Let the mass of each of the identical discs be $m$ and given in the question is the initial angular velocity ${\omega _0}$.
So, the initial angular momentum$ = m \times 0 + m \times {\omega _0} = m{\omega _0}$

Let the final angular velocity of the attached disc is $\omega '$. When the top disc sticks to the bottom disc then the total mass is $\left( {m + m} \right) = 2m$.
The final angular momentum is $2m \times \omega ' = 2m\omega '$.
From the conservation of angular momentum we get,
$m{\omega _0} = 2m\omega ' \\
\Rightarrow \omega ' = \dfrac{{{\omega _0}}}{2} \\ $
Now, the initial rotational kinetic energy is given as ${K_0}$.
${K_0} = \dfrac{1}{2}m{\left( {{\omega _0}} \right)^2}$
Let the final kinetic energy be $K'$.
Now the final rotational kinetic energy is,
$K' = \dfrac{1}{2} \times 2m{\left( {\omega '} \right)^2}$
Now the final rotational energy in terms of initial is by putting
$\omega ' = \dfrac{{{\omega _0}}}{2}$
$\Rightarrow K' = \dfrac{1}{2} \times 2m \times {\left( {\dfrac{{{\omega _0}}}{2}} \right)^2} \\
\Rightarrow K' = \dfrac{1}{2} \times \dfrac{1}{2}m{\left( {{\omega _0}} \right)^2} \\
\Rightarrow K' = \dfrac{1}{2}{K_0}$
So, the change in rotational kinetic energy is,
$\therefore {K_0} - \dfrac{1}{2}{K_0} = \dfrac{1}{2}{K_0}$

So, the correct option is A.

Note: According to the law of conservation of angular momentum, the initial momentum of any body or bodies is equal to the final momentum. When the disc gets attached to each other their mass changes, eventually getting summed up. But as they act as one, they have one angular velocity.