Question

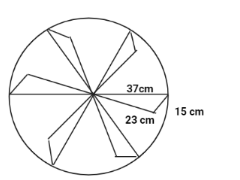
Two identical circles with the same inside design as shown in the figure are to be made at the entrance. The identical triangular leaves are to be painted red and the remaining are to be painted green. Find the total area to be painted red.​

Answer 1

Hint: There are many formulas to find the area of a triangle. But whenever three sides of the triangle are mentioned in the question it's always preferred to use Heron’s formula. In heron’s formula , we first calculate the half of the perimeter of the triangle and then we use this value to further calculate the area.

Complete step by step solution:
Firstly, we should calculate the area of one leaf inside the circle. Here, use heron’s formula:
 $
  a = 37cm \\
  b = 15cm \\
  c = 23cm \;
  $
 $ s = \dfrac{{a + b + c}}{2} $
Now we substitute the values,
 $
  s = \dfrac{{37 + 15 + 23}}{2} \\
  s = \dfrac{{75}}{2} = 37.5 \;
  $
Area of triangle:
 $ = \sqrt {s(s - a)(s - b)(s - c)} $
Substituting the values we will get,
$
   = \sqrt {37.5(37.5 - 37)(37.5 - 15)(37.5 - 28)} \\
   = \sqrt {37.5(0.5)(14.5)(24.5)} \\
   = 78.21c{m^2} \;
  $
Area of one leaf $ = 78.21c{m^2} $
Number of leaf in one design= $ 3 $
Number of leaf in two design= $ 3 \times 2 = 6 $
Then, we can calculate the total area by multiplying 12 with one leaf area.
Area of $ 6 $ leaf
 $
   = 6 \times 78.21 \\
   = 469.26c{m^2} \;
  $
Hence, the total area to be painted red is $ 469.26c{m^2} $ ​.
So, the correct answer is “ $ 469.26c{m^2} $ ”.

Note: Heron’s formula is useful to calculate the area of a triangle only when the triangle is scalene. If it's an isosceles, equilateral or a right angled triangle then we have a simple formula which avoids making our work more tedious.