Question

Two identical charged spheres suspended from a common point by two massless strings of length l are initially a distance d (d << l) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate. As a result the charges approach each other with a velocity v. Then as a function of distance x between them:
\[\begin{align}
  & A.\,v\propto {{x}^{-1/2}} \\
 & B.\,v\propto {{x}^{-1}} \\
 & C.\,v\propto {{x}^{1/2}} \\
 & D.\,v\propto x \\
\end{align}\]

Answer 1

Hint: It becomes easy to solve this question using a free body diagram of the spheres suspended from a common point by two massless strings of length and initially a distance apart. We will be equating the horizontal forces to find the expression of the velocity in terms of the distance.
Formula used:
\[F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{d}^{2}}}\]

Complete answer:
From the given information, we have the data as follows.
Two identical charged spheres suspended from a common point by two massless strings of length l are initially a distance d (d << l) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate.
Consider the free body diagram of spheres.

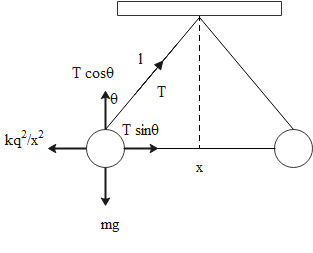
From the above figure, it’s clear that,
\[T\sin \theta =\dfrac{k{{q}^{2}}}{{{x}^{2}}}\] …… (1)
\[T\cos \theta =mg\]…… (2)
Divide the equations (1) and (2).
\[\begin{align}
  & \tan \theta =\dfrac{{}^{k{{q}^{2}}}/{}_{{{x}^{2}}}}{mg} \\
 & \Rightarrow \tan \theta =\dfrac{k{{q}^{2}}}{{{x}^{2}}mg} \\
\end{align}\]
Here \[\tan \theta \approx \theta \], so, \[\theta =\dfrac{k{{q}^{2}}}{{{x}^{2}}mg}\]
Again, we have, \[\dfrac{x}{2l}=\dfrac{k{{q}^{2}}}{{{x}^{2}}mg}\]
\[\begin{align}
  & \Rightarrow {{q}^{2}}=\dfrac{mg{{x}^{3}}}{2kl} \\
 & \Rightarrow q={{\left( \dfrac{mg{{x}^{3}}}{2kl} \right)}^{{1}/{2}\;}} \\
\end{align}\]
The rate of charge leakage equals ‘r’.
\[\begin{align}
  & \therefore \dfrac{dq}{dt}=r \\
 & \Rightarrow \dfrac{dq}{dt}=c\times \dfrac{3}{2}{{x}^{{1}/{2}\;}}\dfrac{dx}{dt}\,\,\,\,\,\,\,\,\,\,\,\left( \dfrac{dx}{dt}=v \right) \\
 & \therefore r=c\sqrt{x}\dfrac{dx}{dt} \\
 & \Rightarrow \dfrac{dx}{dt}=k{{x}^{-1/2}} \\
 & \therefore v\propto \dfrac{1}{\sqrt{x}} \\
\end{align}\]
Or, we can continue the computation as,
\[\begin{align}
  & \Rightarrow q\propto {{c}^{{}^{3}/{}_{2}}} \\
 & \Rightarrow \dfrac{dq}{dt}\propto \dfrac{3}{2}{{x}^{1/2}}\left( \dfrac{dx}{dt} \right) \\
 & \therefore \dfrac{dx}{dt}\propto {{x}^{-1/2}} \\
\end{align}\]
We can solve this problem directly as follows.
We can consider the equation (1) as follows.
\[\begin{align}
  & T\sin \theta =F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{d}^{2}}} \\
 & \tan \theta =\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{x}^{2}}mg} \\
\end{align}\]
Now substitute the expression of the tan of angle as \[\tan \theta =\dfrac{x}{2l}\]in the above equation.
\[\begin{align}
  & \Rightarrow \dfrac{x}{2l}\propto \dfrac{{{q}^{2}}}{{{x}^{2}}} \\
 & \Rightarrow {{q}^{2}}\propto {{x}^{3}} \\
 & \therefore q\propto {{x}^{3/2}} \\
\end{align}\] (as the length is constant value, so, we get a proportionality equation)
Differentiate the above equation. So, we get,
\[\dfrac{dq}{dt}\propto \dfrac{3}{2}{{x}^{1/2}}\dfrac{dx}{dt}\]
Again here \[\dfrac{dx}{dt}\]is constant.
\[\begin{align}
  & \dfrac{dq}{dt}\propto \dfrac{3}{2}{{x}^{1/2}}\dfrac{dx}{dt} \\
 & \Rightarrow v\propto {{x}^{-1/2}} \\
\end{align}\]
\[\therefore \]The velocity in terms of the distance is \[v\propto {{x}^{-1/2}}\]

Thus, option (A) is correct.

Note:
The relation between the velocity and the distance is a derivation formula. We should know that the rate of charge leakage is constant and the velocity is constant to continue the computation.