Question

When two identical batteries of internal resistance 1 $\Omega$ each are connected in series across a resistor R, the rate of heat production in R is $J_1$. When the same batteries are connected in parallel across R, the rate is $J_2$. If $J_1 = 2.25 J_2$ then the value of R in $\Omega$ is?

Answer 1

Hint: When two batteries are connected in a serial fashion, there electromotive forces (emf) add. When two batteries are connected in a parallel fashion, the potential difference across all the batteries is the same; they all drive the same current in the circuit.
Formula used:
Equivalent resistance in series combination:
$R = R_1 + R_2$ .
Equivalent resistance in parallel combination:
$\dfrac{1}{R} = \dfrac{1}{R_1} \dfrac{1}{R_2}$ .
Heat produced across a resistance R given as:
$H = I^2 R t$
when current flows in through R.

Complete answer:
To determine the heat produced we will require the currents in given two different situations.

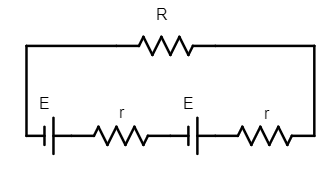
1. For the case when the two identical batteries with emf E, we will get a total emf of 2E in the circuit when the two are connected serially.
The equivalent resistance in the entire circuit becomes
$R_{eq} = 2r + R $.
So the current flowing in the circuit will be:
$I_1 = \dfrac{2E}{2r +R}$.

2. When the two batteries are connected in parallel, the total emf in the circuit will be E only, while the internal resistances will give an equivalent
$r_{eq} = \dfrac{r \times r}{r + r} = \dfrac{r}{2}$.

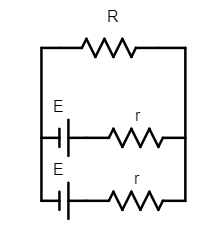
The current flowing in the circuit can be written as:
$I_2 = \dfrac{E}{\dfrac{r}{2} +R}$.

Now, the ratio of heat produced in the two cases can be written as:
$\dfrac{J_1}{J_2} = \dfrac{I_1^2 Rt}{I_2^2 Rt} = \dfrac{I_1^2}{I_2^2} = 2.25$
(as $J_1 = 2.25 J_2$ is given).
We can take square root and write:
$\dfrac{I_1}{I_2} = 1.5$.
On keeping the values we get;
$\dfrac{2E/(2r +R)}{E/( \dfrac{r}{2} +R )} = 1.5$
$\implies \dfrac{r + 2R}{2r +R} = \dfrac{3}{2}$
where we replaced 1.5 by 3/2.
This will give us:
$2r + 4R = 6r + 3R$
$\implies R = 4r$.
As, the internal resistance has a value of 1 $\Omega$, therefore the value of resistance R is 4 $\Omega$.

Note:
When the two batteries were connected parallely we made an attempt to to replace the combination by equivalent internal resistance and equivalent emf. When the emfs were connected in series, we simply combined all the resistances where the voltage drop was occurring.