Question

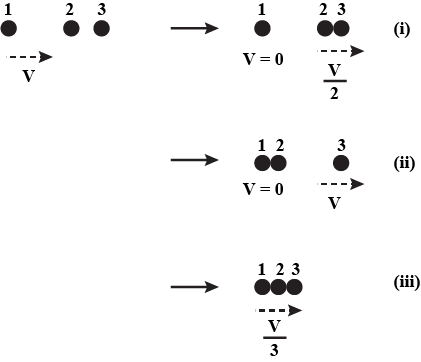
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed \[V\]. If the collision is elastic, which of the following (figure above) is a possible result after collision?

Answer 1

Hint: This question is based on the properties of elastic collision. Elastic collision is a type of collision in which there is no net loss in kinetic energy in the system while the collision takes place. Momentum as well as kinetic energy is conserved quantities in the case of elastic collisions.

Complete answer:
From the law of conservation of momentum,
We can say that the total momentum before collision and the total momentum after collision remains the same.
We also know that for an elastic collision, the total kinetic energy before and after the collision is also the same.
Let the mass of each ball bearing be $m$.
Now, the kinetic energy before the collision takes place is,
$ = \dfrac{1}{2}m{V^2} + \dfrac{1}{2}(2m) \times {0^2}$
$ = \dfrac{1}{2}m{V^2}$
Case number 1:
The kinetic energy after the collision takes place is,
$ = \dfrac{1}{2} \times m \times 0 + \dfrac{1}{2}(2m){\left( {\dfrac{V}{2}} \right)^2}$
$ = \dfrac{1}{2}(2m)\left( {\dfrac{{{V^2}}}{4}} \right)$
On further solving,
$ = \dfrac{1}{4}m{V^2}$
So, clearly the kinetic energy is not conserved in case number 1.
Case number 2:
The kinetic energy after the collision takes place is,
\[ = \dfrac{1}{2} \times 2m \times 0 + \dfrac{1}{2}m{V^2}\]
On further solving,
\[ = \dfrac{1}{2}m{V^2}\]
So, clearly the kinetic energy is conserved in case number 2.
Case number 3:
The kinetic energy after the collision takes place is,
$ = \dfrac{1}{2} \times 3m \times {\left( {\dfrac{V}{3}} \right)^2}$
$ = \dfrac{1}{2} \times 3m \times \left( {\dfrac{{{V^2}}}{9}} \right)$
On further solving,
$ = \dfrac{1}{6}m{V^2}$
So, clearly the kinetic energy is not conserved in case number 3.
So, only case number 2 is possible as it is the only case in which the kinetic energy is conserved.

Note: It is important to note that a frictionless surface is a surface where no friction is present. Practically frictionless surfaces are not possible but for easy calculations some surfaces are considered frictionless.