Question

Two glass plates are separated by water. If surface tension of water is \[75dyn{\text{ }}c{m^{ - 1}}\] and the area of each plate wetted by water is $8c{m^2}$ and the distance between the plates is $0.12mm$ , then the force applied to separate the two plates is:
A. \[{10^{ - 2}}dyne\]
B. \[{10^4}dyne\]
C. \[{10^5}dyne\]
D. \[{10^6}dyne\]

Answer 1

Hint: Use the excess pressure formula to find the pressure lowered between the plates i.e.
$P = {T}{R}$
Here, T is the surface tension of water
R is the radius of the two surfaces due to which the pressure is lowered.
In simple words we will put the values in the equation to get the required force applied to separate the two plates.

Complete answer:

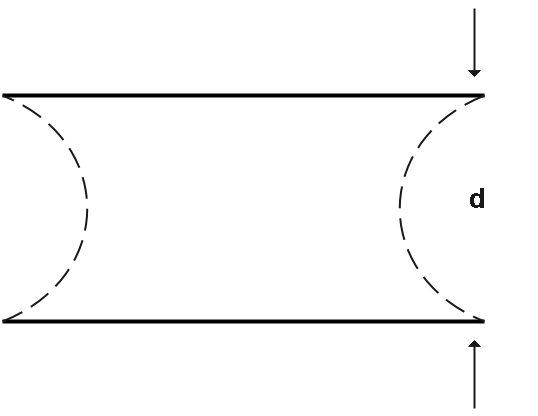
Here we can see the shape of the water layer between the two plates.
Thickness of the film, $d = 0.012cm$
Pressure of the cylindrical face, $R = {d}{2}$
Now, pressure across the surface,
$P = \fdrac{T}{R}$
$\Rightarrow P = {{2T}}{d} $
Area of each plate wetted by water, $A$
And we know that force required to separate the two plate is,
$F = pressure \times area$
$\Rightarrow F = {{2T}}{d}A$
Now, substituting the values in above equation we get,
$F = {{2T}}{d}A$
$\Rightarrow F = {{2 \times 75 \times 8}}{{0.012}}$
$\Rightarrow F = {10^5}dyne$
So, the force applied to separate the two plates is ${10^5}dyne$ .

Hence, the correct option is C.

Note:
Here the curved surface is a cylinder with radius R. Since this behaves as an air bubble in water that is why we have taken the radii to be equal. Otherwise, one should calculate the excess pressure using the radii of the given shape which is not a cylinder or spherical as an air bubble.