Question

Two forces $\vec{F_{1}}=500N$ due east and $\vec{F_{2}}=250N$ due north has their common initial point. $\vec{F_{2}}-\vec{F_{1}}$ is

A.)$250\sqrt{5}N,\; tan^{-1}(2)W$ of $N$
B.)$250N,\; tan^{-1}(2)W$ of $N$
C.)Zero
D.)$750N,\; tan^{-1}(\dfrac{3}{4})N$ of $W$

Answer 1

Hint: In order to solve this question, we need to know about the vector addition, that is the resultant vector $\vec{F_{R}}=\vec{F_{1}}+\vec{F_{2}}$ and vector subtraction, that is $\vec{F_{R}}=\vec{F_{1}}-\vec{F_{2}}=\vec{F_{1}}+(-\vec{F_{2}})$.

We can also notice that the answers have been given in magnitude and angle format. So, we will have to find the magnitude and angle of the two-dimensional vector. Let us consider a two-dimensional vector $\vec{F}=x\hat{i}+y\hat{j}$, where x and y are its components, then the magnitude and angle can be found out using the formulae,

Magnitude, $|\vec F|=|\sqrt{x^2+y^2}|$
Angle, $\theta=tan^{-1}(\dfrac{y}{x})$

Complete step by step solution
We have been given the two vectors $\vec{F_{1}}=500N$ due east and $\vec{F_{2}}=250N$ due north. Let us first draw a two-dimensional vector diagram using the given vectors

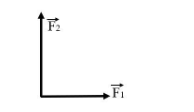
Now, the resultant of the two forces, $\vec{F_{R}}=\vec{F_{2}}-\vec{F_{1}}$
Which we can also write as $\vec{F_{R}}=\vec{F_{2}}+(-\vec{F_{1}})$. We can draw the vector diagram for this as follows,

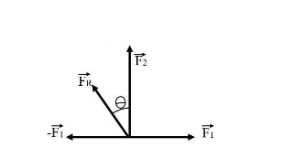
Thus, we can now write $\vec{F_{2}}=500\hat{i}$ and $\vec{F_{1}}=250\hat{j}\\
\therefore \vec{F_{R}}=250\hat{j}+(-500\hat{i})\\
\implies \vec{F_{R}}=250(\hat{j}-2\hat{i})$

Now, the magnitude of the $\vec{F_R}$ can be found using the formula for a two-dimensional $|\vec{F}|=|\sqrt{x^2+y^2}|$ where x and y are its components,

Therefore, $|\vec{F}|=|250\sqrt{1^2+2^2}| \implies |\vec{F}|=250\sqrt{5}$

And the angle $\theta$ of a two-dimensional vector can be found using the formula $\theta=tan^{-1}\dfrac{y}{x}$ where x and y are its components,

Therefore, $\theta= tan^{-1}\dfrac{-2}{1}\implies \theta=-tan^{-1}(2)$ when the reference is due East.

or, $\theta= tan^{-1}(2)\;W$ of $N$

Thus, $\vec{F_{2}}-\vec{F_{1}}=250\sqrt{5}N,\; tan^{-1}(2)W$ of $N$

Hence, option a is the correct answer.

Addition information: In a three-dimensional vector, the directions are denoted by $\hat{i}$, $\hat{j}$ and $\hat{k}$. Cross product and dot product are two very common operations that are involved in vector calculation.

If we assume two vectors $\vec{u}$ and $\vec{v}$, then
Cross product, $\vec{u}\times \vec{v}=uv\;sin\theta$
Dot product, $\vec{u}.\vec{v}=uv\;cos\theta$

Note: We must be careful while finding the angle of a vector regarding its line of reference. In this question also, we saw that the angle value will be different when the reference is taken as East and when taken as N. We often make the mistake in putting the sign according to this and reach the conclusion without checking the reference.