Question

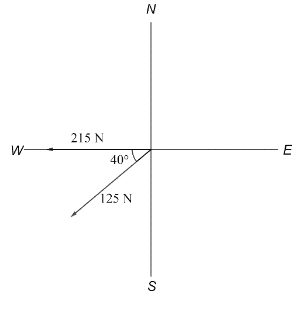
Two forces of $ 125\;N $ and $ 215\;N $ act on an object, as shown in the diagram. Calculate the magnitude and direction (including a specific angle $ \theta $ ) of the resultant force and the equilibrant force?

Answer 1

Hint : To find the resultant force we need to divide the given forces into its respective horizontal and vertical components. By taking the sum of the components, we can find the resultant force. The equilibrant force is the force required to balance the resultant force.
Magnitude of resultant force $ f=\sqrt{{{f}_{x}}^{2}+{{f}_{y}}^{2}} $
Direction of resultant force $ \theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right) $

Complete Step By Step Answer:
Here, we are given two forces with magnitude as $ f_1=215N $ and $ f_2=125N $
As the direction of the forces are different, we cannot decide the resultant force by simply adding the magnitudes.
Hence, to find the resultant magnitude, we must split the forces into the respective vertical and horizontal component.
The angle of the force for the components should always be taken from the positive $ x $ -axis.
Hence, the force $ f_1=215N $ makes an angle $ \theta =180{}^\circ $ with the positive $ x $ -axis.
Hence, the components for the force can be expressed as
 $ {{f}_{1x}}={{f}_{1}}\cos 180{}^\circ =(215)(-1)=-215 $
 $ {{f}_{1y}}={{f}_{1}}\sin 180{}^\circ =(215)(0)=0 $
Similarly the force $ f_2=125N $ makes an angle $ \theta =180{}^\circ +40{}^\circ =220{}^\circ $ with the positive $ x $ -axis
Hence, the components for the force can be expressed as
 $ {{f}_{2x}}={{f}_{2}}\cos 220{}^\circ =(125)(-0.766)=-95.75 $
 $ {{f}_{2y}}={{f}_{2}}\sin 220{}^\circ =(125)(-0.643)=-80.35 $
Now, the resultant horizontal and vertical component are in the same direction, hence they can be obtained by simple addition
 $ {{f}_{x}}={{f}_{1x}}+{{f}_{2x}} $
Substituting the given values,
 $ \therefore {{f}_{x}}=-215-95.75 $
 $ \therefore {{f}_{x}}=-310.75 $
For the vertical component,
 $ {{f}_{y}}={{f}_{1y}}+{{f}_{2y}} $
Substituting the given values,
 $ \therefore {{f}_{y}}=0-80.35 $
 $ \therefore {{f}_{y}}=-80.35 $
Now, the magnitude of the resultant force is given by
 $ f=\sqrt{{{f}_{x}}^{2}+{{f}_{y}}^{2}} $
Substituting the obtained values,
 $ f=\sqrt{{{\left( -310.75 \right)}^{2}}+{{\left( -80.35 \right)}^{2}}} $
 $ f=320.97N $
The direction of the resultant force is given by,
 $ \theta ={{\tan }^{-1}}\left( \dfrac{{{f}_{y}}}{{{f}_{x}}} \right) $
Substituting the obtained values,
 $ \therefore \theta ={{\tan }^{-1}}\left( \dfrac{-80.35}{-310.75} \right) $
 $ \therefore \theta =14.5{}^\circ $
Here, both the forces are in the third quadrant and both the components are also negative. Hence, their resultant force must lie in the third quadrant. As the answer obtained is in the first quadrant, we can add or subtract the period of tangent function to get the correct resultant direction.
 $ \therefore \theta =14.5{}^\circ -180{}^\circ $
 $ \therefore \theta =-165.5{}^\circ $
Hence, the resultant force can be expressed as
 $ {{\vec{f}}_{r}}=320.97N\angle -165.5{}^\circ $
Now, the equilibrant force is the force that balances the resultant force. Thus it is of the same magnitude and in the opposite direction
 $ \therefore {{\vec{f}}_{e}}=320.97N\angle 14.5{}^\circ $

Note :
While calculating the direction of the resultant force, the sign of the components must be considered along with the resultant sign of the inverse tangent function. If both the components are negative, the resultant answer will be positive, but as the components are negative, the direction will be in the third quadrant. Similarly if the sign of both components is different, the resultant answer will be negative. Hence, by considering the signs of the components, the quadrant of the resultant should be decided.