Question

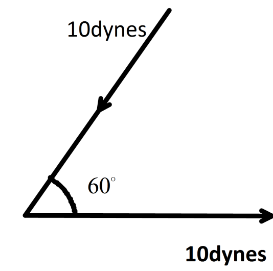
Two forces each numerically equal to \[10\,dynes\] are acting as shown in the following figure, then their resultant is :
A. \[10\,dynes\]
B. \[20\,dynes\]
C. \[10\sqrt 3\,dynes\]
D. \[5\,dynes\]

Answer 1

Hint: Use the concept of the triangle law of vectors. Study and learn how to calculate the resultant of two vectors. Any quantity which has magnitude along with direction is a vector. Some examples for vector quantities are displacement, velocity, acceleration, force, pressure, etc.

Formula used:
The resultant of two vectors making with each other an angle \[\theta \] is equal to,
\[R = \sqrt {{A^2} + {B^2} + 2AB\cos \theta } \]
where \[A\] and \[B\] are the two vectors and \[R\] is the magnitude resultant vector of the two.
The angle between the resultant vector and one of the vectors,
\[\alpha = {\tan ^{ - 1}}\dfrac{{b\sin \theta }}{{a + b\cos \theta }}\]

Complete step by step answer:
Here, we have given two forces of \[10\,dynes\] acting with each other at an angle \[{60^ \circ }\]. Now, we know that the resultant of two vectors \[A\] and \[B\] making an angle \[\theta \] is \[R = \sqrt {{A^2} + {B^2} + 2AB\cos \theta } \].

So, putting , the value of first vector\[A = 10dynes\], second vector\[B = 10dynes\]and angle between them \[\theta = {60^ \circ }\] we have,
\[R = \sqrt {{{10}^2} + {{10}^2} + 2 \times 100 \times \cos {{60}^ \circ }} \]
Now, we know, cosine of \[\theta = {60^ \circ }\] is equal to \[\dfrac{1}{2}\]
So, putting the value and further simplifying we have,
\[R = \sqrt {200 + 100} \]
\[\Rightarrow R = \sqrt {300} \]
\[\therefore R = 10\sqrt 3 \]
Hence the magnitude of the resultant vector is \[10\sqrt 3 \,dynes\].

Hence, option C is the correct answer.

Note: The triangle law of vectors states that, if a body is acted upon by two vectors represented by the two sides of a triangle taken in consecutive order, the resultant vector is represented by the third side of the triangle. Here, the third side is along the end of the one vector and the start of the other vector. The angle between the resultant vector and any vector \[A\]is given by, \[\alpha = {\tan ^{ - 1}}\dfrac{{B\sin \theta }}{{A + B\cos \theta }}\].Putting the value we will have finally, \[\alpha = {\tan ^{ - 1}}\dfrac{2}{{\sqrt 3 }}\] .