Question

Two equilateral triangles with sides \[4\,cm\] and \[6\,cm\] are _____________ triangles.

Answer 1

Hint: Here in this question, they have given two triangles and it is an equilateral triangle. The length of the equilateral triangle is known. We have to consider the proportion for the sides of the two triangles and then we have determined what kind of the triangles are they. Hence we obtain the required solution for the given question.

Complete step-by-step answer:
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. Based on the lengths or the sides of the triangle, it is divided into 3 different kinds. They are equilateral triangle, isosceles triangle and scalene triangle.
Equilateral triangle, where all the sides of the triangle are same
Isosceles triangle, where any two sides of the triangle are same or equal.
Scalene triangle, where all the sides of the triangle are different.
Now consider the question, two equilateral triangles with the sides \[4\,cm\] and \[6\,cm\]. Let we consider the two triangles namely \[\vartriangle ABC\] and \[\vartriangle PQR\]
Since it is an equilateral triangle each and every side are equal. Therefore in the \[\vartriangle ABC\], \[AB = BC = CA = 4\,\,cm\] and in the \[\vartriangle PQR\], \[PQ = QR = RP = 6\,\,cm\].

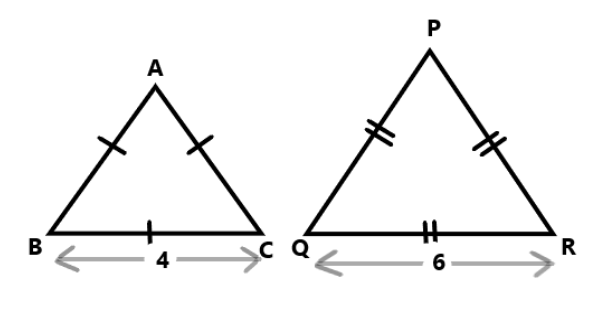
Now let us determine the ratios for the sides of the triangle.
\[\dfrac{{AB}}{{PQ}} = \dfrac{4}{6} = \dfrac{2}{3}\], \[\dfrac{{BC}}{{QR}} = \dfrac{4}{6} = \dfrac{2}{3}\] and \[\dfrac{{AC}}{{PR}} = \dfrac{4}{6} = \dfrac{2}{3}\]. Therefore, the ratios of sides of triangles are equal.
Hence corresponding sides of both the triangles are in proportion to each other. By the definition of similar triangles, we can conclude that two equilateral triangles with sides \[4\,cm\] and \[6\,cm\] are similar triangles. i.e., \[\vartriangle ABC \] ∼ \[\vartriangle PQR\]
So, the correct answer is “Similar triangles”.

Note: The definition of similar triangles is given by two triangles are similar if they have the same ratio of corresponding sides. These triangles have the same shape but size will be different. To simplify the ratio we must know about the simple multiplication and division. The symbol to represent the similar is ∼