Question

Two equal vectors $\overline{A}$ and $\overline{B}$ acting at angle $\theta $ with each other then show that the resultant vector bisects the angle $\theta $.

Answer 1

Hint: Resultant of two vectors is found by the parallelogram law of vectors. According to this law the two given vectors are considered as two adjacent sides of a parallelogram and the parallelogram is completed. The diagonal of this parallelogram is the resultant of these two vectors.

Formula used:
$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$
$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$
$\tan \alpha =\dfrac{\text{opposite side}}{\text{adjacent side}}$
$\sin \theta =2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}$
$1+\cos \theta =2{{\cos }^{2}}\dfrac{\theta }{2}$


Complete step by step answer:
Consider two vectors $\overline{A}$ and $\overline{B}$with equal magnitudes. The angle between the vectors is $\theta $. Let the magnitude of both vectors be ‘a’.

The resultant of these two vectors is given by the law of parallelogram. The resultant of the vectors is the diagonal of the parallelogram formed by considering the two vectors as adjacent sides of this parallelogram. The direction of the resultant points away from the vertex of the vectors, as shown in the figure.

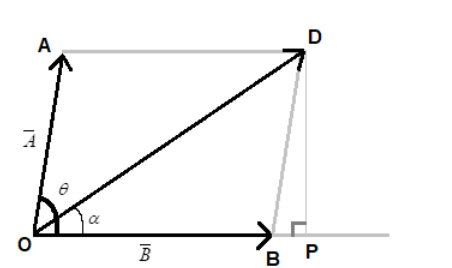
Now, let the resultant make an angle $\alpha $ with vector $\overline{B}$. Drop a perpendicular on vector $\overline{B}$ from point D. Let the foot of this perpendicular be P as shown.

Since opposite sides of a parallelogram are equal, AO and DB, both are equal to a. $\Delta DBP$ is a right-angled triangle with DB as hypotenuse. Since AO and DB are parallel, $\angle DBP$ is equal to $\theta $. We will use the trigonometric ratios $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$.
In this triangle,
$\sin \theta =\dfrac{DP}{DB}=\dfrac{DP}{a}\Rightarrow DP=a\sin \theta $
$\cos \theta =\dfrac{BP}{DB}=\dfrac{BP}{a}\Rightarrow BP=a\cos \theta $
Now consider the right-angled $\Delta DOP$. Here,
$\tan \alpha =\dfrac{\text{opposite side}}{\text{adjacent side}}=\dfrac{DP}{OP}=\dfrac{a\sin \theta }{a+a\cos \theta }=\dfrac{\sin \theta }{1+\cos \theta }$
$\Rightarrow \tan \alpha =\dfrac{\sin \theta }{1+\cos \theta }$ ……..(i)
Let us use the half angle formulas.
$\sin \theta =2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}$ and $1+\cos \theta =2{{\cos }^{2}}\dfrac{\theta }{2}$
Substitute these values in equation (i).
Therefore, $\tan \alpha =\dfrac{2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}}{2{{\cos }^{2}}\dfrac{\theta }{2}}=\dfrac{\sin \dfrac{\theta }{2}}{\cos \dfrac{\theta }{2}}=\tan \dfrac{\theta }{2}$
$\Rightarrow \tan \alpha =\tan \dfrac{\theta }{2}$
Therefore, $\alpha =\dfrac{\theta }{2}$.
Hence proved that the resultant of two vectors with equal magnitudes bisects the angle between two vectors.

Note: If you know the properties of a parallelogram then this problem is very simple to solve. As discussed, we find the resultant by drawing a parallelogram taking the two vectors as adjacent sides of the parallelogram. When the adjacent sides of a parallelogram are equal, it becomes a rhombus. The diagonal of a rhombus bisects the angles of the parallelogram. Therefore, the resultant bisects the angle between the vectors.