Question

Two equal discs are in contact on a table. A third disc of same mass but of double radius strikes them symmetrically and remains at rest after impact. The coefficient of restitution is:

A. \[\dfrac{2}{3}\]
B. \[\dfrac{1}{3}\]
C. \[\dfrac{9}{{16}}\]
D. \[\dfrac{{\sqrt 3 }}{2}\]

Answer 1

Hint:Use the law of conservation of linear momentum and the formula for linear momentum of an object. First determine the final velocity of the two discs after collision along the line of collision and the sine of angle made by the radius of the third disc with the horizontal. Use the formula for co- efficiency of restitution. Substitute the values of velocity of separation and velocity of approach along the line of collision and determine the final answer.
Formulae used:
The expression for law of conservation of linear momentum is
\[{P_i} = {P_f}\] …… (1)
Here, \[{P_i}\] is the initial linear momentum of the object and \[{P_f}\] is the final linear
momentum of the object.
The linear momentum \[P\] of an object is given by
\[P = mv\] …… (2)
Here, \[m\] is the mass of the object and \[v\] is the velocity of the object.
The coefficient of restitution is given by
\[e = \dfrac{{{\text{velocity of separation}}}}{{{\text{velocity of approach}}}}\] …… (3)

Complete step by step answer:
We have given that the radius of the two discs in contact is and the radius of the third disc is double of the radius of two discs.
Let \[R\] be the radius of two discs in contact and \[2R\] be the radius of the third disc.
Let \[u\] be the initial speed of the third disc before collision.
The diagram of the three disc when they collide with each other is as follows:

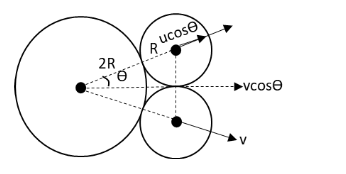
In the above diagram, \[u\] is the initial velocity of the third disc and \[v\] is the velocity of the two discs in contact after collision. The velocity of the third disc along the line of collision is \[u\cos \theta \].
From the above diagram,
\[\sin \theta = \dfrac{R}{{3R}}\]
\[ \Rightarrow \sin \theta = \dfrac{1}{3}\]
Before collision, the two discs which are in contact are stationary. Hence, their initial linear
momentum is zero.
After collision, the third disc stops and the two discs start moving along the line of collision.
Let us apply the law of conservation of linear momentum to the discs before and after collision along the horizontal direction.
\[mu = mv\cos \theta + mv\cos \theta \]
\[ \Rightarrow u = 2v\cos \theta \]
\[ \Rightarrow v = \dfrac{u}{{2\cos \theta }}\]
The velocity of separation along the line of collision after collision is \[v\].
The velocity of approach along the line of collision after collision is \[u\cos \theta \].
Let us now determine the coefficient of restitution.
Substitute \[v\] for \[{\text{velocity of separation}}\] and \[u\cos \theta \] for \[{\text{velocity of
approach}}\] in equation (3).
\[e = \dfrac{v}{{u\cos \theta }}\]
Substitute \[\dfrac{u}{{2\cos \theta }}\] for \[v\] in the above equation.
\[e = \dfrac{{\dfrac{u}{{2\cos \theta }}}}{{u\cos \theta }}\]
\[ \Rightarrow e = \dfrac{1}{{2{{\cos }^2}\theta }}\]
\[ \Rightarrow e = \dfrac{1}{{2\left( {1 - {{\sin }^2}\theta } \right)}}\]
\[ \Rightarrow e = \dfrac{1}{{2\left( {1 - {{\left( {\dfrac{1}{3}} \right)}^2}} \right)}}\]
\[ \Rightarrow e = \dfrac{1}{{2\left( {1 - \dfrac{1}{9}} \right)}}\]
\[ \Rightarrow e = \dfrac{9}{{16}}\]
Therefore, the coefficient of restitution is \[\dfrac{9}{{16}}\].
Hence, the correct option is C.

Note: The students should keep in mind that in the formula for coefficient of restitution the velocity of approach of the third disc before collision and velocity of the two discs from the third disc after collision must be along the line joining the centres of the third disc and two discs which is the line of collision for discs and not along the horizontal direction.