Question

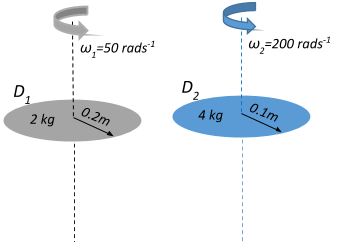
Two discs are rotating about their axes normal to the discs and passing through the centres of the discs. Disc $D_1$ has $2\;kg$ mass and $0.2\;m$ radius and the initial angular velocity of $50\;rads^{-1}$. Disc $D_2$ has $4\;kg$ mass and $0.1\;m$ radius and initial angular velocity of $200\;rads^{-1}$. The two discs are brought in contact face to face, with their axes of rotation coincident. The final angular velocity (in $rads^{-1}$) of the system is:
A. 40
B. 60
C. 100
D. 120

Answer 1

Hint: Begin by determining the moment of inertia of the two discs, for axes passing perpendicular to their surface. Then, use the relation between moment of inertia and angular velocity to find their angular momenta. Add the two individual momenta to get the total initial angular momentum.
Now, when they are brought in contact with each other, the two discs behave as one massive unit. In this case, determine the sum of their moments of inertia and obtain an expression for the total final angular momentum of the system. Use the conservation of angular momentum principle to equate the two expressions and arrive at the appropriate angular speed of the collective motion of the discs.

Formula Used:
MI of disc: $I = \dfrac{1}{2}mr^2$
Angular momentum: $L=I\omega$
Conservation of angular momentum: $L_i=L_f$

Complete Step-by-Step Solution:
We are given that for,
Disc $D_1$: $m_1=2\;kg$, $r_1=0.2\;m$ and $\omega_1=50\;rads^{-1}$
Disc $D_2$: $m_2=4\;kg$, $r_2=0.1\;m$ and $\omega_2=200\;rads^{-1}$

We know that the moment of inertia MI of a circular disc about an axis perpendicular to the disc and passing through the centre O is given as:
$I = \dfrac{1}{2}mr^2$

Therefore, for Disc $D_1$: $I_1 = \dfrac{2\times 0.2^2}{2} = 0.04\;kgm^2$, and
Disc $D_2$: $I_2 = \dfrac{4\times 0.1^2}{2} = 0.02\;kgm^2$

Now, the angular momentum of a disc is given as:
$L=I\omega$

The total initial angular momentum of two discs will be the sum of their individual angular momenta, i.e.,
$L_i = I_1\omega_1 + I_2\omega_2$
$\Rightarrow L_i = (0.04\times 50)+(0.02\times 200) = 2+4=6\;kgm^2s^{-1}$

Now, the two discs are brought in contact face to face, with their axes of rotation coincident. This means that the moment of inertia of the system becomes the sum of their individual moments of inertia. This results in the two discs moving with a new mutual angular velocity, say $\omega$.

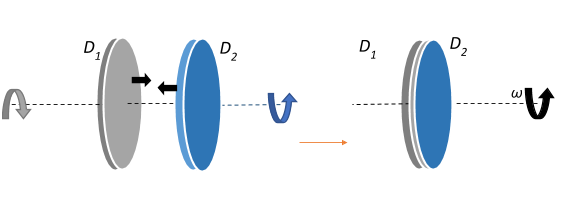
The total final angular momentum of the system of two discs in contact with each other will be,
$L_f = (I_1+I_2)\omega = (0.04+0.02)\omega = 0.06\omega\; kgm^2s^{-1}$

We now need to determine the final angular velocity. For this, we proceed as follows.

According to the law of conservation of angular momentum, for any isolated system, the total initial and final angular momentum will remain constant, i.e.,
$L_i=L_f$
$\Rightarrow 6 = 0.06\omega$
$\Rightarrow \omega=\dfrac{6}{0.06} = 100\;rads^{-1}$

Therefore, the correct choice would be C.100

Note:
It is important to understand the collective behaviour of components and the factors that get influenced under their non-individualistic behaviour. We add up the moments of inertia in the second case to signify the repositioning of the centre of mass of the entire system, since it now behaves as a collective unit with the two discs working together. This also influences their rotatory motion which is why we get a kind of a superposed final angular speed.
Also, always pay attention to the mentioned axis of rotation, since the expression for the moment of inertia for the same object will differ if it has a different axis of rotation. Suppose the axis of rotation of the disc was at the rim of the disc, then its moment of inertia would be $I = \dfrac{3}{2}mr^2$, or if its axis of rotation was along the diameter of the disc, it would be $I=\dfrac{1}{4}mr^2$ and so on.