Question

Two cross roads, each of width $5m$ , run at the right angles through the centre of a rectangular park of length $70m$ and breadth $45m$ and parallel to its sides. Find the area of the roads. Also find the cost of constructing the roads at the rate of $Rs.105$ per ${m^2}$

Answer 1

Hint: We will divide the rectangle into $4$ equal rectangle and one central square which when combined together makes up the roads. The width of the road is $5m$ , Length of the park is $70m$ and the width of the park is $45m$ . Using this information, we can easily solve the given problem.

Formula Used:
We will use the basic formulas of the area of a rectangle and then basic multiplication.
Area of rectangle $ = l \times b$
where $l$ - length of rectangle
and $b$ - breadth of rectangle.

Complete answer:
Let us first draw a diagram from the given data for a clear idea.

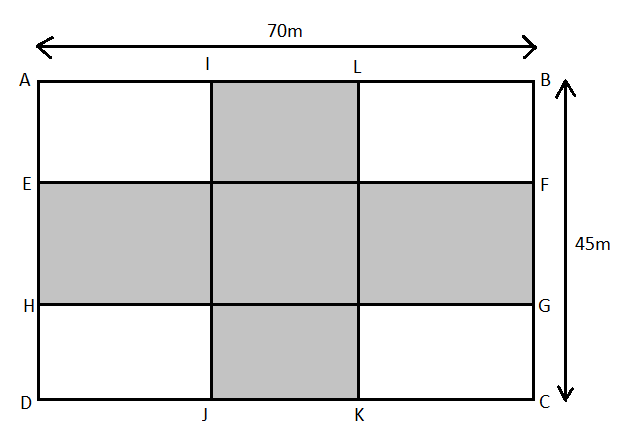
Here $ABCD$ is the rectangular park and $IJKL$ and $EFGH$ are the crossroads.
We know that the length of the first parallel road as given in the question is $ = 70m$
So, the area of the first road $ = 70m \times 5m = 350{m^2}$
Now we will be calculating for the second road:
Since the length of the second road as given in the question is \[ = 45m\]
Then the area of the second road $ = 45m \times 5m = 225{m^2}$
Now we will calculate the area of the common part:
So, the area of the common part of cross road with $5m$ width that lies at the
centre of the park.
\[5m \times 5m\]=\[25{m^2}\]
Now we calculate the area of road which will be calculated by the concept that is described below
Area of roads $ = $ Area of first road $ + $ Area of second cross road−Common area
$\left( {350{m^2} + 225{m^2}} \right) - 25{m^2}$
 Since the cost of the construction per ${m^2}$ $ = Rs.105$
$550 \times 105 = 57750$
Thus, we have found the total cost as $Rs.57750$
Therefore, the required cost of constructing the roads at the rate of $Rs.105$ per ${m^2}$ is $Rs.57750$

Note:
While doing the calculation a rough figure is expected to be made in order to clarify the question and get the proper calculation method and an idea of a diagram which will be helpful for the better understanding of the question. The calculation must be made correct.