Question

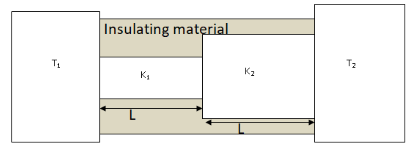
Two conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures \[{T_1} = 300\,{\text{K}}\] and \[{T_2} = 100\,{\text{K}}\] as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are \[{K_1}\] and \[{K_2}\] respectively. If the temperature at the junction of the two cylinders in the steady state is \[200\,{\text{K}}\]. Then \[\dfrac{{{K_1}}}{{{K_2}}} = \_\_\_\_\_\].

Answer 1

Hint: Here we are asked to find the ratios of conductivities of smaller and the larger cylinders. First write down the given information. You will need to use here the formula for rate of heat transfer to an object, use this formula to find out the heat transfer in both the cylinders and apply the condition for steady state to find out the required ratio.

Complete step by step answer:
Given, temperatures of heat baths \[{T_1} = 300\,{\text{K}}\] and \[{T_2} = 100\,{\text{K}}\].
The thermal conductivities of the materials of the smaller and larger cylinders are \[{K_1}\] and \[{K_2}\] respectively.Lengths of both the cylinders are \[L\]. Temperature of the junction at steady state is \[{T_j} = 200\,{\text{K}}\]. The radius of the larger cylinder is twice that of the smaller one, let the radius of the smaller cylinder be \[{R_1}\] then the radius of the larger cylinder will be \[{R_2} = 2R\].

The rate of heat transfer to an object is given by,
\[\dfrac{{\Delta Q}}{{\Delta t}} = KA\dfrac{{\Delta T}}{d}\] (i)
where \[\Delta Q\] is the amount of heat transfer in time interval \[\Delta t\], \[K\] is the conductivity of the material of the object, \[A\] is the cross sectional area for heat transfer, \[d\] is the length through which heat transferred and \[\Delta T\] is the temperature difference between two ends of the object.
Now, we find out the heat transfer for both the cylinders separately,
For smaller cylinder,
\[K = {K_1}\], \[L = L\], \[A = \pi {R_1}^2\] and \[\Delta T = {T_1} - {T_j}\]
Putting this values in equation (i), we get the rate of heat transfer in smaller cylinder as,
\[\dfrac{{\Delta {Q_1}}}{{\Delta t}} = {K_1}\left( {\pi {R_1}^2} \right)\dfrac{{\left( {{T_1} - {T_j}} \right)}}{L}\] (ii)
For larger cylinder,
\[K = {K_2}\], \[L = L\], \[A = \pi {R_2}^2\] and \[\Delta T = {T_2} - {T_j}\]
Putting this values in equation (i), we get the rate of heat transfer in larger cylinder as,
\[\dfrac{{\Delta {Q_2}}}{{\Delta t}} = {K_2}\left( {\pi {R_2}^2} \right)\dfrac{{\left( {{T_j} - {T_2}} \right)}}{L}\] (iii)
As, the system is inside insulating material there is no loss to heat to surrounding and also in steady state there will be no accumulation of heat which means at steady state at the junction will be have,
\[\dfrac{{\Delta {Q_1}}}{{\Delta t}} = \dfrac{{\Delta {Q_2}}}{{\Delta t}}\]
Now, putting the values from equations (ii) and (iii) in the above equation we have,
\[{K_1}\left( {\pi {R_1}^2} \right)\dfrac{{\left( {{T_1} - {T_j}} \right)}}{L} = {K_2}\left( {\pi {R_2}^2} \right)\dfrac{{\left( {{T_j} - {T_2}} \right)}}{L}\]
\[ \Rightarrow \dfrac{{{K_1}}}{{{K_2}}} = \left( {\pi {R_2}^2} \right)\dfrac{{\left( {{T_j} - {T_2}} \right)}}{L} \times \dfrac{L}{{\left( {\pi {R_1}^2} \right)\left( {{T_1} - {T_j}} \right)}}\]
\[ \Rightarrow \dfrac{{{K_1}}}{{{K_2}}} = {\left( {\dfrac{{{R_2}}}{{{R_1}}}} \right)^2}\dfrac{{\left( {{T_j} - {T_2}} \right)}}{{\left( {{T_1} - {T_j}} \right)}}\]
Now, putting the values of \[{R_2}\], \[{T_1}\], \[{T_2}\] and \[{T_j}\] we get
\[\dfrac{{{K_1}}}{{{K_2}}} = {\left( {\dfrac{{2{R_1}}}{{{R_1}}}} \right)^2}\dfrac{{\left( {200 - 100} \right)}}{{\left( {300 - 200} \right)}}\]
\[ \Rightarrow \dfrac{{{K_1}}}{{{K_2}}} = 4\dfrac{{\left( {100} \right)}}{{\left( {100} \right)}}\]
\[ \therefore \dfrac{{{K_1}}}{{{K_2}}} = 4\]

Therefore, we get \[\dfrac{{{K_1}}}{{{K_2}}} = 4\].

Note: Factors that affect the transfer of heat or heat flow through an object are conductivity of the material of the object, the cross sectional area, the temperature difference between both ends of the object and the length through which the heat is transferred. Also remember the point that insulators are bad conductors of heat that is why in the given question there was no loss of heat to surrounding as the system was inside insulating material.