Question

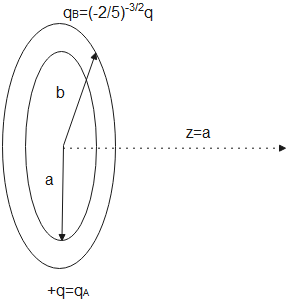
Two concentric rings, one of radius ‘a’ and the other of radius ‘b’ have the charges +q an${\left( {\dfrac{{ - 2}}{5}} \right)^{\dfrac{{ - 3}}{2}}}q$ respectively as shown in the figure. Find the ratio b/a if a charge particle placed on the axis at z=a is in equilibrium.

Answer 1

Hint: Charge is uniformly distributed over the circular ring structure. But on the bigger ring some positive charge is distributed and on the smaller ring different positive charge is distributed. We have a formula to find out the electric field due to the ring on the axial point. We will find out and apply equilibrium conditions to solve this.

Formula used: $E = \dfrac{{kQz}}{{{{\left( {{z^2} + {r^2}} \right)}^{\dfrac{3}{2}}}}}$

Complete step by step answer:
We were given two rings and we were told that any particle placed at an axial point which is at a distance ‘a ‘ from the center of the rings is in equilibrium. The kind of charge distributed on the bigger ring is negative while the kind of charge distributed on the inner smaller ring is positive. So on the axial point there will be right side force due to the inner ring while there will be left side force due to the outer ring. Both will cancel out each other and equilibrium condition is attained.
The electric field due to inner ring is
$\eqalign{
  & E = \dfrac{{kQz}}{{{{\left( {{z^2} + {r^2}} \right)}^{\dfrac{3}{2}}}}} \cr
  & \therefore {E_i} = \dfrac{{kqa}}{{{{\left( {{a^2} + {a^2}} \right)}^{\dfrac{3}{2}}}}}\mathop i\limits^ \wedge \cr} $
Where r is the radius and Q is the charge distributed on the ring and ‘z’ is the axial distance.
The electric field due to outer ring is
$\eqalign{
  & E = \dfrac{{kQz}}{{{{\left( {{z^2} + {r^2}} \right)}^{\dfrac{3}{2}}}}} \cr
  & \therefore {E_o} = \dfrac{{k{{\left( {\dfrac{{ - 2}}{5}} \right)}^{\dfrac{{ - 3}}{2}}}qa}}{{{{\left( {{a^2} + {b^2}} \right)}^{\dfrac{3}{2}}}}}\mathop i\limits^ \wedge \cr} $
Since that is equilibrium point we have
$\eqalign{
  & {E_i} + {E_o} = 0 \cr
  & \Rightarrow \dfrac{{kqa}}{{{{\left( {{a^2} + {a^2}} \right)}^{\dfrac{3}{2}}}}}\mathop i\limits^ \wedge + \dfrac{{k{{\left( {\dfrac{{ - 2}}{5}} \right)}^{\dfrac{{ - 3}}{2}}}qa}}{{{{\left( {{a^2} + {b^2}} \right)}^{\dfrac{3}{2}}}}}\mathop i\limits^ \wedge = 0 \cr
  & \Rightarrow {a^2} + {b^2} = \left( {\dfrac{5}{2}} \right) \times 2{a^2} \cr
  & \Rightarrow b = 2a \cr
  & \therefore \dfrac{b}{a} = 2 \cr} $

Hence the ratio of radii will be 2.

Note: Since the charge distribution is uniform the y components of circular structure get cancelled and only x components get added up. Hence we had only x component of electric field for both the rings and no y component. For complete rings of the same charge distribution, the field at center will be zero.