Question

Two concentric circles are of radii 5cm and 3cm. Find the length of the chord of the larger circle which touches the smaller circle.

Answer 1

Hint: This problem deals with concentric circles and the most important Pythagoras theorem. Concentric circles are those circles which are inscribed one inside the other, which means that both the circles have a common center. Pythagora's theorems are only applicable to right angled triangles. Given a right angled with AB, BC and AC be the height, base and the hypotenuse of the triangle respectively. Then,
 $ \Rightarrow A{B^2} + B{C^2} = A{C^2} $

Complete step-by-step answer:
Given that there are two concentric circles.
Also given that the small circle which is inside the big circle has a radius of 3 cm, and the radius of the big circle is 5 cm.
The chord of the bigger circle touches the smaller circle, which means that the chord of the bigger circle is a tangent to the smaller circle.
The picture is shown as given below:

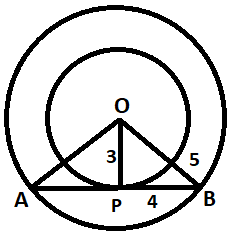
The radius of the smaller circle = 3 cm
The radius of the bigger circle = 5 cm
The center of both the circles is O. The chord of the bigger circle is AB.
When drawn a normal to the tangent of the smaller circle at P, which is also the chord AB, of the bigger circle.
Now the $ \Delta OPB $ is a right angled triangle. Hence the $ \Delta OPB $ should satisfy the Pythagoras theorem.
 $ \Rightarrow O{P^2} + P{B^2} = O{B^2} $
Here OP is the radius of the smaller circle which is 3 cm.
 $ \Rightarrow OP = 3 $ cm
OB is the radius of the bigger circle which is 5 cm.
 $ \Rightarrow OB = 5 $ cm
Hence substituting the above values in the Pythagoras theorem:
 $ \Rightarrow {3^2} + P{B^2} = {5^2} $
 $ \Rightarrow 9 + P{B^2} = 25 $
 $ \Rightarrow P{B^2} = 16 $
Applying square root on both sides of the above equation:
 $ \therefore PB = 4 $
Now the $ \Delta OAP $ is also a right angled triangle. Hence the $ \Delta OAP $ should satisfy the Pythagoras theorem.
 $ \Rightarrow O{P^2} + P{A^2} = O{A^2} $
Here OP is the radius of the smaller circle which is 3 cm.
 $ \Rightarrow OP = 3 $ cm
OB is the radius of the bigger circle which is 5 cm.
 $ \Rightarrow OA = 5 $ cm
Hence substituting the above values in the Pythagoras theorem:
 $ \Rightarrow {3^2} + P{A^2} = {5^2} $
 $ \Rightarrow 9 + P{A^2} = 25 $
 $ \Rightarrow P{A^2} = 16 $
Applying square root on both sides of the above equation:
 $ \therefore PA = 4 $ cm
Hence the length of the chord AB is the sum of PA and PB:
 $ \Rightarrow AB = PA + PB $
 $ \Rightarrow AB = 4 + 4 $
 $ \therefore AB = 8 $
The length of the chord AB is 8 cm.

Final answer: The length of the chord of the larger circle which touches the smaller circle is 8 cm.

Note:
Please note that this problem can also be done in another way but with a slight change, which is described here. Instead of considering the other triangle which is on another side of the normal OP, of the tangent AB. We can just decide that the length of PA is also the same as PB which is 4 cm, as the normal to the tangent bisects the chord AB.