Question

Two coils each of 100 turns are held such that one lies in a vertical plane and the other in the horizontal plane with their centers coinciding. The radius of the vertical coil is $ 0.20m $ and that of the horizontal coil is $ 0.30m $ . How will you neutralize the magnetic field of the earth at their common center? If the summation of current to be passed through coil is $ {{i}_{total}}=xA $ . Find $ {{x}^{*}}10 $. Horizontal component of earth’s magnetic field $ =0.35\times {{10}^{-4}}T $ and angle of dip $ =30{}^\circ $.

Answer 1

Hint: First of all, using the given data we will consider the vertical component of earth’s magnetic field, then we will consider a net magnetic field opposite to the magnetic field of earth and then we will find the value of its horizontal and vertical components and then on basis of it we can find the net magnetic field.

Formula used: $ \tan \theta =\dfrac{{{B}_{v}}}{{{B}_{h}}} $

Complete step-by-step answer:
In the question it is given that two coils each of 100 turns are held such that one lies in a vertical plane and the other in the horizontal plane with their centers coinciding. The radius of the vertical coil is $ 0.20m $ and that of the horizontal coil is $ 0.30m $ and we are asked to neutralize the magnetic field of earth at common center, so, for that first of all we will draw a rough figure which can be shown as,

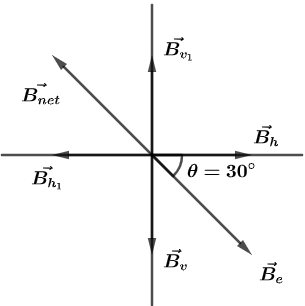
Now, with the help of figure, we can see the horizontal component of earth’s magnetic field and dip angle, so from that we will find the vertical component of earth’s magnetic field by using the formula,
 $ \tan \theta =\dfrac{{{B}_{v}}}{{{B}_{h}}} $
Where, $ {{B}_{v}} $ is the vertical component of magnetic field of the Earth, $ \theta $ is dip angle and $ {{B}_{h}} $ is the horizontal component of earth’s magnetic field.
In question it is given that dip angle $ \theta ={{30}^{\circ }} $ and $ {{B}_{h}}=0.35\times {{10}^{-4}} $
Substituting these values, we will get,
 $ \tan {{30}^{\circ }}=\dfrac{{{B}_{v}}}{0.35\times {{10}^{-4}}} $
 $ \Rightarrow {{B}_{v}}=0.35\times {{10}^{-4}}\times \dfrac{1}{\sqrt{3}}=0.202\times {{10}^{-4}}T $
Now, we can assume a net magnetic field acting in the opposite direction to the magnetic field of the Earth and then we will consider its vertical component which is equal and opposite to $ {{B}_{v}} $ and its horizontal component is equal and opposite to $ {{B}_{h}} $ . This can be seen mathematically as,
Horizontal component of net magnetic field $ {{B}_{h1}}={{B}_{h}} $ and Vertical component of net magnetic field $ {{B}_{v1}}={{B}_{v}} $ .
Now, the value of vertical and horizontal components of net magnetic field can be obtained by using the formula,
 $ B=\dfrac{{{\mu }_{0}}i}{2R} $ …………………….(i)
Where, $ {{\mu }_{0}}=4\pi \times {{10}^{-7}} $ , I is current and R is the radius of the loop.
So, using this expression we will find the value of currents, which can be given as,
 $ {{B}_{{{v}_{1}}}}=\dfrac{{{\mu }_{0}}{{i}_{1}}}{2{{R}_{1}}}={{B}_{v}} $ ……………….(ii)
 $ {{B}_{{{h}_{1}}}}=\dfrac{{{\mu }_{0}}{{i}_{2}}}{2{{R}_{2}}}={{B}_{h}} $ ……………………..(iii)
Further, simplifying we will find the value of currents,
${{i}_{1}}=\dfrac{2{{R}_{1}}{{B}_{v}}}{{{\mu }_{0}}}=\dfrac{2\times 0.3\times 0.202\times {{10}^{-4}}}{4\pi \times {{10}^{-7}}}=0.0111A $
$ {{i}_{2}}=\dfrac{2{{R}_{2}}{{B}_{h}}}{{{\mu }_{0}}}=\dfrac{2\times 0.2\times 0.35\times {{10}^{-4}}}{4\pi \times {{10}^{-7}}}=0.0964A $
Thus it can be said that $ 0.0111A $ current should pass in the horizontal coil and $ 0.0964A $ current should pass in the vertical coil to neutralize the Earth’s magnetic field.

Note: Students must take care while considering the dip angle because they might consider the angle from vertical component instead of horizontal component and due to that the whole sum will go wrong and they will not get the desired answer so they must take care while solving such problems.