Question

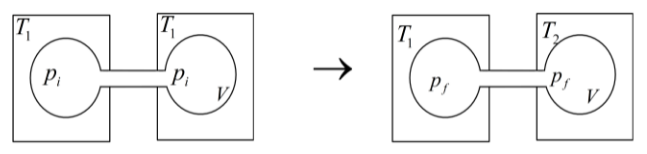
Two closed bulbs of equal volume (\[V\]) containing an ideal gas initially at pressure \[{p_i}\] and temperature \[{T_1}\] are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to \[{T_2}\]. What is the final pressure \[{p_f}\]?

Answer 1

Hint:Use Ideal gas equation to find the number of moles of gas in the chambers before and after mixing of the gas and solve for the final pressure. Ideal gas equation states that the ratio of product of pressure and volume to the product of gas constant and absolute temperature of the gas is equal to the number of moles of the gas.

Formula used:
Ideal gas equation is given by,
\[n = \dfrac{{pV}}{{RT}}\]
where, \[n\] is the number of moles of the gas present in the volume, \[V\] is the volume of the gas , \[R\] is the universal gas constant and \[T\] is the temperature of the gas.

Complete step by step answer:
We have been given here, that the gas is at a pressure \[{p_i}\] and temperature \[{T_1}\] is connected through the narrow tube with negligible volume. So, the gas gets mixed and the pressure changes in the process when the temperature is raised to \[{T_2}\]. So, the number of moles before and after the process will be the same.

Now, equation of state of ideal gas is given by, \[n = \dfrac{{pV}}{{RT}}\] where, \[n\] is the number of moles of the gas present in the volume, \[V\] is the volume of the gas , \[R\] is the universal gas constant and \[T\] is the temperature of the gas. So, using ideal gas equation the numbers of moles of gas present in the bulbs is,
\[{n_i} = \dfrac{{{p_i}V}}{{R{T_1}}} + \dfrac{{{p_i}V}}{{R{T_1}}}\]
\[\Rightarrow {n_i} = \dfrac{{2{p_i}V}}{{R{T_1}}}\]
After the temperature raise the numbers of moles of gas present is,
\[{n_f} = \dfrac{{{p_f}V}}{{R{T_1}}} + \dfrac{{{p_f}V}}{{R{T_2}}}\]

So, according to the condition given equation numbers of moles of gas will be same,
Hence we can write, \[{n_i} = {n_f}\]
Putting the values we have,
\[\dfrac{{2{p_i}V}}{{R{T_1}}} = \dfrac{{{p_f}V}}{{R{T_1}}} + \dfrac{{{p_f}V}}{{R{T_2}}}\]
\[\Rightarrow \dfrac{{2{p_i}V}}{{R{T_1}}} = \dfrac{{{p_f}V}}{R}\left( {\dfrac{1}{{{T_1}}} + \dfrac{1}{{{T_2}}}} \right)\]
Up on simplifying we have,
\[{p_f} = \dfrac{{\dfrac{{2{p_i}V}}{{{T_1}}}}}{{\left( {\dfrac{1}{{{T_1}}} + \dfrac{1}{{{T_2}}}} \right)}}\]
\[\therefore {p_f} = \dfrac{{2{p_i}V{T_2}}}{{({T_1} + {T_2})}}\]

Hence, final pressure \[{p_f}\] is \[\dfrac{{2{p_i}V{T_2}}}{{({T_1} + {T_2})}}\].

Note: The number of moles of gas present in bulbs remains always constant since the volume of the gas is not getting changed and the mole number depends on the pressure and the temperature of the gas in the chamber. Also note that for final condition number of moles of gas in the left chamber is \[\dfrac{{{p_f}V}}{{R{T_1}}}\] and in the right chamber it is \[\dfrac{{{p_f}V}}{{R{T_2}}}\].