Question

Two circular pieces of equal radii and maximum area, touching each other are cut out from rectangular card board of dimensions \[14cm \times \,7cm\] . Find the area of remaining card board.

Answer 1

Hint: We can draw a figure and place 2 circles having same radii and maximum area. Then we can find the radius from the dimensions of the rectangle. Then we can find the area of the rectangle and circle separately and then subtract them to get the required area.

Complete step by step answer:

We can draw a rectangle with the given dimension\[14cm \times \,7cm\]. Then the diameter of the largest circle that can be drawn will be equal to the breadth of the rectangle. As the length is twice the breadth one more circle with the same radius can be placed in the rectangle.

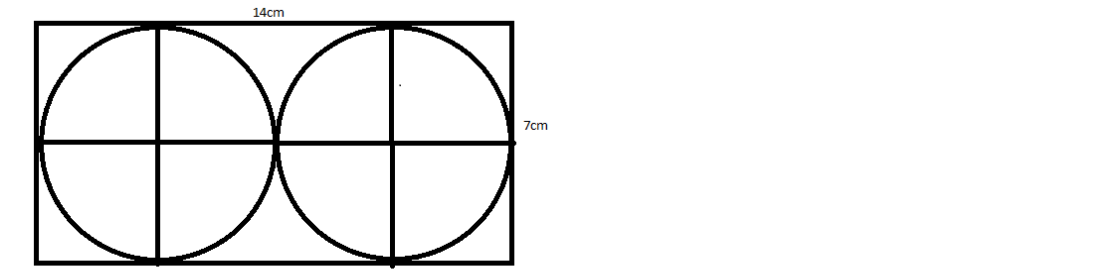
Now we can find the area of the rectangle.
Its dimensions are given as \[14cm \times \,7cm\]
The area of the rectangle is given by the equation$A = l \times b$. On substituting the values, we get,
$ \Rightarrow A = 14 \times 7$
$ \Rightarrow A = 98c{m^2}$
Now we can find the area of the circle. From the figure, we can understand that the diameter is 7cm.
So, the radius is given by $r = \dfrac{d}{2}$
$ \Rightarrow r = \dfrac{7}{2}$
Now area of a circle is given by the equation$\,a = \pi {r^2}$. On substituting the value of radius, we get,
$ \Rightarrow a = \dfrac{{22}}{7}{\left( {\dfrac{7}{2}} \right)^2}$
On simplification, we get,
$ \Rightarrow a = \dfrac{{77}}{2}$
This is the area of one circle. So to get the required area, we must subtract twice the area of the circle from the area of the rectangle. So the required area is given by,
$Area = A - 2a$
On substituting the values we get,
$ = 98 - 2 \times \dfrac{{77}}{2}$
On simplification we get,
$ = 98 - 77$
$ = 21c{m^2}$
Therefore the area of remaining cardboard is $21c{m^2}$


Note: Drawing a diagram helps in the better understanding of this problem. As the length of the rectangle is twice its breadth, we can split it as 2 equal squares. Then the circle with largest area inside each square can be inserted. It will have a diameter equal to the side length of the square. Then we can find the area of the circle and subtract from the total area to get the required answer. We must make sure that all the units are written and do necessary conversions if required.