Question

Two circular coils of radii $5cm$ and $10cm$ carry equal currents of $2A$. The coils have $50$ and $100$ turns respectively, and are placed in such a way that their planes as well as their centres coincide. Magnitude of magnetic field at the common centre of coils is
A. $8\pi \times {{10}^{-6}}T$ if current in the coils are in the same sense
B. $4\pi \times {{10}^{-6}}T$ if current in the coils are in opposite sense
C. Zero if current in coils are in opposite sense
D. $8\pi \times {{10}^{-6}}T$ if current in the coils are in opposite sense

Answer 1

Hint: We will calculate the value of magnetic field intensity by each coil and depending on the direction of current through the coils; resultant magnetic field varies at the common centre of the coils.

Formula used:
$B=\dfrac{{{\mu }_{o}}ni}{2r}$

Complete step by step answer:
When a current carrying conductor is formed into a loop or several loops to form a coil, a magnetic field develops that flows through the centre of the loop or coil along its longitudinal axis and circles back along the outside of the coil. The magnetic field generated by separate turns of wire all pass through the centre of the coil and add up to produce a strong field there. The more turns of the wire, the stronger the field produced.
Magnetic field through a current carrying coil is given by:
$B=\dfrac{{{\mu }_{o}}ni}{2r}$
Where,
${{\mu }_{o}}$ is the permeability constant
$n$ is the number of turns in coil
$i$ is the current through coil
$r$ is the radius of coil
We are given two circular coils of radii 5 cm and 10 cm having 50 and 100 turns respectively.

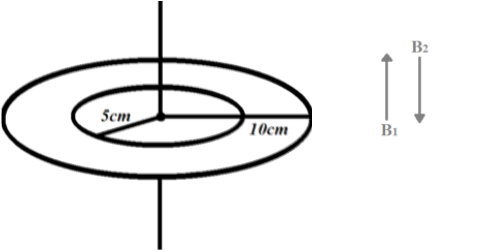
Magnetic field through coil one,
${{B}_{1}}={{n}_{1}}\dfrac{{{\mu }_{o}}{{i}_{1}}}{2{{r}_{1}}}$
Magnetic field through coil second,
${{B}_{2}}={{n}_{2}}\dfrac{{{\mu }_{o}}{{i}_{2}}}{2{{r}_{2}}}$
If currents are in the same direction,
$B={{B}_{1}}+{{B}_{2}}$
$B=\dfrac{{{\mu }_{o}}i}{2}\left( \dfrac{{{n}_{1}}}{{{r}_{1}}}+\dfrac{{{n}_{2}}}{{{r}_{2}}} \right)$
Putting the values, we get,
$\begin{align}
  & B=\dfrac{4\times {{10}^{-7}}\times 2}{2}\times \left( \dfrac{5}{50}+\dfrac{10}{100} \right)\times \dfrac{1}{{{10}^{-2}}} \\
 & B=8\pi \times {{10}^{-6}}T \\
\end{align}$
If currents are in opposite direction,
$B={{B}_{1}}-{{B}_{2}}$
$B=\dfrac{{{\mu }_{o}}i}{2}\left( \dfrac{{{n}_{1}}}{{{r}_{1}}}-\dfrac{{{n}_{2}}}{{{r}_{2}}} \right)$
Putting the values, we get,
$\begin{align}
  & B=\dfrac{4\times {{10}^{-7}}\times 2}{2}\times \left( \dfrac{5}{50}-\dfrac{10}{100} \right)\times \dfrac{1}{{{10}^{-2}}} \\
 & B=0 \\
\end{align}$
Therefore, when current in the coils are in the same sense, then resultant magnetic field is $8\pi \times {{10}^{-6}}T$ and when current in the coils are in opposite sense, then resultant magnetic field is zero.

Hence, the correct options are A and C.

Note:
While calculating the magnetic field by a current carrying coil, direction of current should be considered since the magnetic field is a vector quantity. Depending on the direction of current through different coils, resultant magnitude of magnetic field varies at the common centre of the coils.