Question

Two circles whose radii are equal to 4 and 8 intersect at right angles. The length of their common chords is \[\dfrac{\lambda }{{\sqrt 5 }}\] , then find \[\lambda \] .

Answer 1

Hint: When any two sides of the triangle intersect at right angles, we use Pythagoras theorem to find the missing sides. In this question the length of the common chord will be equal to the double the height of the triangle so first we will find the height of the triangle and then we will find the common cord to compare it with \[\dfrac{\lambda }{{\sqrt 5 }}\] to find its value.

Complete step-by-step answer:
Given the radius of the circles
 \[
  OA = {r_1} = 4 \\
  AC = {r_2} = 8 \;
 \]

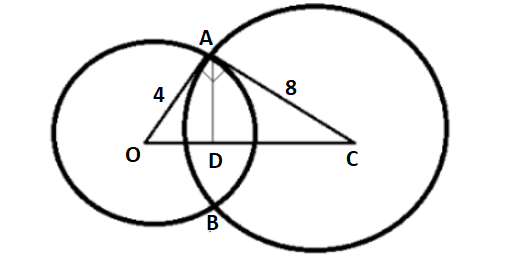
Now we will first find the distance between the center of the two circles which is OC and since the radii of the two circle intersects at right angle so we will use Pythagoras theorem to find OC by
 \[
\Rightarrow O{C^2} = O{A^2} + A{C^2} \\
\Rightarrow OC = \sqrt {{4^2} + {8^2}} \\
\Rightarrow OC = \sqrt {16 + 64} \\
   = \sqrt {80} \\
   = 4\sqrt 5 \;
 \]
From the figure we can say the length of a common cord of the two circles will be equal to the double the height of the triangle and let us assume the height of the triangle is \[AP = x\]

Now in triangle AOC since it is a right angled triangle so the area of the triangle will be
 \[
\Rightarrow area\left( {\Delta AOC} \right) = \dfrac{1}{2} \times 4 \times 8 \\
   = 16 - - (i) \\
 \]
Now again if we consider OC as the base of the triangle AOC then AP will be the height also the
 \[
\Rightarrow area\left( {\Delta AOC} \right) = \dfrac{1}{2} \times 4\sqrt 5 \times x \\
   = 2\sqrt 5 x - - (ii) \;
 \]
Now we will equate the equations (i) and (ii), we can say
 \[
\Rightarrow 2\sqrt 5 x = 16 \\
\Rightarrow x = \dfrac{8}{{\sqrt 5 }} \;
 \]
Now since the length of a common chord of the two circles is equal to the double the height of the triangle so
 \[\Rightarrow 2x = \dfrac{{16}}{{\sqrt 5 }} - - (iii)\]
Now in the question it is already given length of their common chords is \[\dfrac{\lambda }{{\sqrt 5 }}\] so by comparing this length from equation (iii), we can say
 \[\lambda = 16\]
So, the correct answer is “16”.

Note: Another method to find the common chord of two intersecting circles is by using the concept of family of circles where family of curve passing through the points of intersection of the circles S1 and S2 is represented by the equation \[{S_1} + \lambda {S_2} = 0\] . The line passing through the intersection of the two circles will represent the equation of the common chord.