Question

Two circles touch each other internally. The sum of their area is \[130\pi c{{m}^{2}}\] and the distance between their centers is 8 cm. Find the radii of the two circles.

Answer 1

Hint: Draw a diagram of the two circles touching internally. Assume the radius of the bigger circle as R and radius of the smaller circle as r. Take the difference of their radius and equate it with the 8 to first relation between the two radii. Now, apply the formula for area of circle given as: - Area = \[\pi \times {{\left( radius \right)}^{2}}\] and take the sum of their areas and equate it with \[130\pi \] to second relation between the two radii. Solve the two equations to get the value of R and r.

Complete step by step solution:
Here we have been provided with two circles that are touching internally with the distance between their radii as 8 cm and their sum of areas is \[130\pi c{{m}^{2}}\]. We have been asked to determine the radius of the two circles. First let us draw a diagram depicting the given situation.

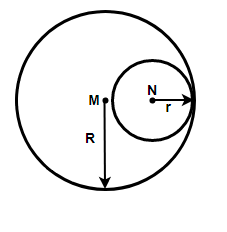
In the above figure we have assumed two circles with centre M and N. The bigger circle is having radius R and the smaller circle is having radius r. Now, it is given that the distance between the centers of the two circles is 8 cm.
$\Rightarrow $ MN = 8
We know that the distance between the centers of two circles touching internally is the difference between their radii. So we have,
\[\Rightarrow R-r=8\] - (1)
Further it is given that the sum of their area is \[130\pi c{{m}^{2}}\]. So applying the formula for the area of a circle given as Area = \[\pi \times {{\left( radius \right)}^{2}}\] we get,
$\Rightarrow $ A = Area of bigger circle = \[\pi {{R}^{2}}\] and a = area of smaller circle = \[\pi {{r}^{2}}\]
Taking the sum of areas of the two circles and equating it with \[130\pi \] we get,
\[\begin{align}
  & \Rightarrow \pi {{R}^{2}}+\pi {{r}^{2}}=130\pi \\
 & \Rightarrow \pi \left( {{R}^{2}}+{{r}^{2}} \right)=130\pi \\
\end{align}\]
Cancelling the common factor $\pi $ from both the sides we get,
\[\Rightarrow \left( {{R}^{2}}+{{r}^{2}} \right)=130\] - (2)
Substituting the value of R from equation (1) in equation (2) we get,
\[\begin{align}
  & \Rightarrow {{\left( 8+r \right)}^{2}}+{{r}^{2}}=130 \\
 & \Rightarrow 64+{{r}^{2}}+16r+{{r}^{2}}=130 \\
 & \Rightarrow 2{{r}^{2}}+16r-66=0 \\
\end{align}\]
Dividing both the sides with 2 we get,
\[\Rightarrow {{r}^{2}}+8r-33=0\]
Using the middle term split method to factor the above quadratic expression we get,
\[\begin{align}
  & \Rightarrow {{r}^{2}}+11r-3r-33=0 \\
 & \Rightarrow r\left( r+11 \right)-3\left( r+11 \right)=0 \\
 & \Rightarrow \left( r-3 \right)\left( r+11 \right)=0 \\
\end{align}\]
Substituting each term equal to 0 we get,
$\therefore $ r = 3 or r = –11
Since radius cannot be negative so we can neglect r = –11, therefore r = 3. Substituting r = 3 in equation (1) we get,
$\therefore $ R = 3 + 8 = 11
Hence, the radius of the bigger circle is 11 cm and the radius of the smaller circle is 3 cm.

Note: Do not forget to draw the diagram of the given situation as it will help us to visualize the first condition of the question, i.e. the difference between the two radii, in a better way. Note that wherever possible you must try to cancel the common factors as it will make our calculations easy, like we have cancelled the factor $\pi $ on both the sides and also while solving the quadratic equation we have divided both the sides with 2 so that the coefficient of ${{x}^{2}}$ becomes 1. Also remember that the value of radius cannot be negative so reject the negative value.