Question

Two circles of radii 5cm and 3cm intersect at two points and the distance between their centers is 4cm. Find the length of the common chord.

Answer 1

Hint: Here we draw two intersecting circles and join their centers and join the two intersecting points to form a chord. Prove congruence using SSS rule of congruence in the two triangles formed by the line joining the centers. Prove the congruence in two triangles formed in one side of the circle using SAS congruence rule. Show that chord is bisected by the line joining the centers. After proving AB is perpendicular to PQ, assume length of center to the chord of any circle as a variable and use Pythagoras theorem to find the values of length of chord.

Complete step-by-step answer:
We draw two triangles \[{C_1}\] and \[{C_2}\] having centers 5cm and 3cm respectively.
Center of the circle \[{C_1}\] is P and the center of the circle \[{C_2}\] is Q.
Join the centers of the circles to form PQ
Join the points of intersection of two circles i.e. A and B to form a common chord AB.
Join AP, BP, AQ and BQ.

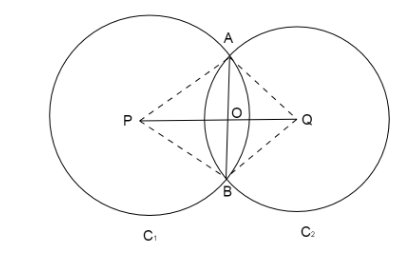
Here \[PA = PB\](radii of\[{C_1}\])
Also, \[QA = QB\] (radii of\[{C_2}\])
We prove congruence between two triangles PAQ and PBQ.
In \[\vartriangle PAQ,\vartriangle PBQ\]
\[PA = PB\](Radii of\[{C_1}\])
\[QA = QB\] (Radii of\[{C_2}\])
\[PQ = PQ\](Common side)
Then, by SSS congruence rule we can say \[\vartriangle PAQ \cong \vartriangle PBQ\]
Since we know two congruent triangles have corresponding sides and corresponding angles equal.
We can write \[\angle APQ = \angle PBQ\]
\[ \Rightarrow \angle APO = \angle BPO\] … (1)
We prove congruence between two triangles PAO and PBO.
In \[\vartriangle PAO,\vartriangle PBO\]
\[PA = PB\](Radii of\[{C_1}\])
\[\angle APO = \angle BPO\](From equation (1))
\[PO = PO\](Common side)
Then, by SAS congruence rule we can say \[\vartriangle PAO \cong \vartriangle PBO\]
Since we know two congruent triangles have corresponding sides and corresponding angles equal.
We can write \[\angle POA = \angle POB\] and \[AO = BO\] … (2)
Now we know sum of angles on a straight line is \[{180^ \circ }\]
We take the sum of angles on line AB.
\[ \Rightarrow \angle POA + \angle POB = {180^ \circ }\]
Substitute \[\angle POA = \angle POB\]
\[ \Rightarrow \angle POA + \angle POA = {180^ \circ }\]
\[ \Rightarrow 2\angle POA = {180^ \circ }\]
Divide both sides by 2
\[ \Rightarrow \dfrac{{2\angle POA}}{2} = \dfrac{{{{180}^ \circ }}}{2}\]
Cancel the same terms from numerator and denominator.
\[ \Rightarrow \angle POA = {90^ \circ }\]
Then we can say AB is perpendicular to PQ.
Therefore, \[\angle AOP = \angle BOP = \angle BOQ = \angle AOQ = {90^ \circ }\]
Let us assume the length\[OP = x\], then \[OQ = 4 - x\](As the length of\[PQ = 4\])
Now we apply Pythagoras theorem in right angled\[\vartriangle AOP\]
\[A{O^2} + O{P^2} = A{P^2}\]
Substitute the value of\[OP = x\] and \[AP = 5\]
 \[ \Rightarrow A{O^2} + {x^2} = {(5)^2}\]
\[ \Rightarrow A{O^2} + {x^2} = 25\]
Shift the variable to RHS of the equation
\[ \Rightarrow A{O^2} = 25 - {x^2}\] … (3)
Now we apply Pythagoras theorem in right angled \[\vartriangle AOQ\]
\[A{O^2} + O{Q^2} = A{Q^2}\]
Substitute the value of \[OQ = 4 - x\] and \[AQ = 3\]
 \[ \Rightarrow A{O^2} + {(4 - x)^2} = {(3)^2}\]
\[ \Rightarrow A{O^2} + {(4 - x)^2} = 9\]
Shift the variable to RHS of the equation
\[ \Rightarrow A{O^2} = 9 - {(4 - x)^2}\] … (4)
Equate the values of \[A{O^2}\] from equations (3) and (4)
\[ \Rightarrow 25 - {x^2} = 9 - {(4 - x)^2}\]
Shift all variable to one side of the equation
\[ \Rightarrow 25 - 9 = - {(4 - x)^2} + {x^2}\]
Open the value in RHS using the property \[{(a - b)^2} = {a^2} + {b^2} - 2ab\]
\[ \Rightarrow 16 = - \left( {{4^2} + {x^2} - 2 \times 4 \times x} \right) + {x^2}\]
\[ \Rightarrow 16 = - \left( {16 + {x^2} - 8x} \right) + {x^2}\]
Multiply the minus sign inside the bracket
\[ \Rightarrow 16 = - 16 - {x^2} + 8x + {x^2}\]
Cancel the terms in RHS with same magnitude but opposite sign
\[ \Rightarrow 16 = - 16 + 8x\]
Shift constant values to one side of the equation
\[ \Rightarrow 16 + 16 = 8x\]
\[ \Rightarrow 32 = 8x\]
Divide both sides of the equation by 8
\[ \Rightarrow \dfrac{{32}}{8} = \dfrac{{8x}}{8}\]
Cancel the same factors from numerator and denominator on both sides of the equation.
\[ \Rightarrow 4 = x\]
Then, \[OP = 4\]cm
Substitute the value of \[x = 4\] in equation (3)
\[ \Rightarrow A{O^2} = 25 - {(4)^2}\]
\[ \Rightarrow A{O^2} = 25 - 16\]
\[ \Rightarrow A{O^2} = 9\]
Write RHS in such a way that it is a square of a number
\[ \Rightarrow A{O^2} = {3^2}\]
Take square root on both sides of the equation
\[ \Rightarrow \sqrt {A{O^2}} = \sqrt {{3^2}} \]
Cancel square root by square of the values
\[ \Rightarrow AO = 3\]
Now we know from equation (2) \[AO = BO\]
We can write \[AB = AO + BO\]
Substitute the value of \[AO = BO\]
\[ \Rightarrow AB = AO + AO\]
\[ \Rightarrow AB = 2AO\]
Substitute the value of AO as 3cm
\[ \Rightarrow AB = 2 \times 3\]
\[ \Rightarrow AB = 6\]

Therefore, the length of the common chord is 6cm.

Note: * SSS congruence rule states that two triangles are congruent if three sides of one triangle are equal to three corresponding sides of another triangle.
* SAS congruence rule states that two triangles are congruent if two sides and included angle of one triangle is equal to corresponding two sides and included angle of other triangle.
* Pythagoras theorem states that in a right angled triangle, the sum of square of base and square of height is equal to square of the hypotenuse.
If we have a right angled triangle, \[\vartriangle ABC\] with right angle, \[\angle B = {90^ \circ }\]

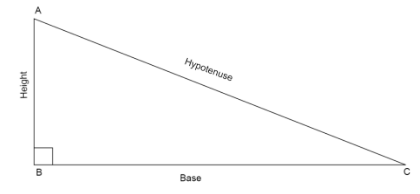
Then using the Pythagoras theorem we can write that \[A{C^2} = A{B^2} + B{C^2}\]