Question

Two circles of equal radiuses a cut orthogonally. If their centres are $(2,3)$ and $(5,6)$, then the radical axis of these circles passes through the point.
A. $(3a,5a)$
B. $(2a,a)$
C. $\left( {a,\dfrac{{5a}}{3}} \right)$
D. $(a,a)$

Answer 1

Hint: According to the question given in the question we have to determine the radical axis of these circles passes through the point when two circles of equal radiuses are cut orthogonally. If there centres are $(2,3)$ and $(5,6)$. So, first of all we have to understand about the intersection of the circles orthogonally which is explained as below:
The meaning of the intersection of two circles orthogonally is that the tangent to each of them makes a right angle at their point of intersection and passes through the centres of both of the circles. We can also understand it with the help of the diagram as mentioned below:

Where, ${C_1},{C_2}$ are the centres of both of the circles and a is the radius which is the same for both of the circles.
Now, as we can see that the radius is the same, so their radical axis will pass through the mid-point of both of the centres.
Now, to determine the distance between the centres we have to use Pythagoras theorem and as we know that the radical axis is perpendicular to the line joining centres and passes through their mid-point so, we can easily determine its equation.
Now, we have to determine the equation of the line which can be determined with the help of the formula of the line equation as given below:

Formula used: $ \Rightarrow (y - {y_1}) = m(x - {x_1})....................(A)$
Where, m is the slope of the line and $({x_1},{y_1})$ are the points of intersection.
Now, after determining the equation we have to check the given options which will satisfy the equation obtained.

Complete step by step solution:
Step 1: First of all we have to determine their radical axis will pass through the mid-point of both of the centres we can easily determine it by finding the mean of the radiuses we can also understand it with the help of the diagram as given below:

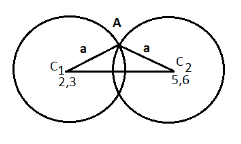
Hence,
$
   \Rightarrow \left( {\dfrac{{2 + 5}}{2},\dfrac{{3 + 6}}{2}} \right) \\
   \Rightarrow \left( {\dfrac{7}{2},\dfrac{9}{2}} \right)
 $
Step 2: Now, we have to determine the distance between the radiuses ${C_1},{C_2}$ which can be determined with the help of Pythagoras theorem as mentioned in the solution hint. Hence,
$
   \Rightarrow a\sqrt 2 = \sqrt {{{(5 - 2)}^2} + {{(6 - 3)}^2}} \\
   \Rightarrow a\sqrt 2 = \sqrt {{3^2} + {3^2}} \\
   \Rightarrow a\sqrt 2 = \sqrt {9 + 9} \\
   \Rightarrow a\sqrt 2 = 3\sqrt 2
 $
Now, on comparing the equation as obtained just above,
$ \Rightarrow a = 3$
Step 3: Now, we have to determine the equation of the line which can be determined with the help of the formula (A) as mentioned in the solution hint.
$ \Rightarrow \left( {y - \dfrac{9}{2}} \right) = m\left( {x - \dfrac{7}{2}} \right)……………………..(1)$
Step 4: Now, as we know that radical axis is perpendicular to the line joining centres and passes through their mid-point so, slope of the line is $m = - 1$hence, on substituting the slope in the equation (1) as obtained in the solution step 3. Hence,
$ \Rightarrow \left( {y - \dfrac{9}{2}} \right) = - 1\left( {x - \dfrac{7}{2}} \right)………………(2)$
Step 5: Now, we have to solve the equation (2) as obtained in the solution step 4.
$
   \Rightarrow (2y - 9) = - (2x - 7) \\
   \Rightarrow 2x + 2y = 9 + 7 \\
   \Rightarrow 2x + 2y = 16 \\
   \Rightarrow x + y = 8..................(3)
 $
Step 6: Now, as can see that option $\left( {a,\dfrac{{5a}}{3}} \right)$satisfies the equation (3) as obtained in the solution step 5. Hence,
$
   \Rightarrow \left( {a + \dfrac{{5a}}{3}} \right) = 8 \\
   \Rightarrow \left( {\dfrac{{3a + 5a}}{3}} \right) = 8 \\
   \Rightarrow \dfrac{{8a}}{3} = 8
 $
Now, on substituting the value of a as we have obtained in the solution step 2 in the equation as obtained just above,
$
   \Rightarrow \dfrac{{8 \times 3}}{3} = 8 \\
   \Rightarrow 8 = 8
 $
Final solution: hence, with the help of the formula (A) as mentioned in the solution hint we have determined the radical axis of these circles passes through the point is $\left( {a,\dfrac{{5a}}{3}} \right)$.

Therefore option (C) is correct.

Note: The intersection of two circles orthogonally is that the tangent to each of them makes a right angle at their point of intersection and passes through the centres of both of the circles.
The radical axis is perpendicular to the line joining centres and passes through their mid-point so, the slope of the line will be $m = - 1$