Question

Two circles each of radius 7cms, intersect each other. The distance between their centers is \[7\sqrt{2}\]cms. Find the area common to both circles.

Answer 1

Hint: Draw a diagram of two circles intersecting each other. Join the centers of the circles with the points of intersection of the circles to form a quadrilateral. Now, find the area of the quadrilateral by dividing it into two right-angle triangles and using the area relation: - Area = \[\dfrac{1}{2}\times \] base \[\times \] height. Subtract the area of this quadrilateral from the sum of areas of two sectors formed. Apply the formula for the area of sectors of the circle given as: - Area = \[\pi {{r}^{2}}\times \left( \dfrac{\theta }{{{360}^{\circ }}} \right)\], where r = radius of circle, ‘\[\theta \]’ is the angle formed between the radius.

Complete step-by-step solution
Here, we have been given that two circles are intersecting each other and we have to find the area common to both the circles. So first, let us draw a diagram of the given situation.

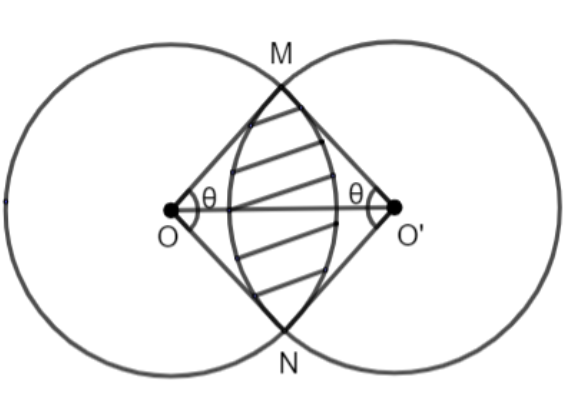
In the above figure, we have taken two circles having centers O and O’ and they are intersecting each other at points M and N. The common area to both the circles is represented by the shaded region.
Now, we have been given that the radius of both the circles is 7cms and the distance between their centers is \[7\sqrt{2}\]cm. So, we have,
In triangle OMO’,
\[\Rightarrow OM=O'M=\]7cm
\[\Rightarrow OO'=7\sqrt{2}\]cm
\[\Rightarrow {{\left( OM \right)}^{2}}+{{\left( O'M \right)}^{2}}={{\left( OO' \right)}^{2}}\]
Therefore, by the converse of Pythagoras theorem the given triangle OMO’ is a right-angle triangle which is right-angled at M. So, \[\angle OMO'={{90}^{\circ }}\].
Similarly, in triangle ONO’,
\[\Rightarrow ON=O'N\]= 7cm
\[\Rightarrow OO'=7\sqrt{2}\]cm
\[\Rightarrow {{\left( ON \right)}^{2}}+{{\left( O'N \right)}^{2}}={{\left( OO' \right)}^{2}}\]
Therefore, by the converse of Pythagoras theorem the given triangle ONO’ is a right-angle triangle which is right-angled at N. So, \[\angle ONO'={{90}^{\circ }}\].
Therefore, the area of the quadrilateral OMO’N is the sum of the area of two triangles, namely OMO’ and ONO’. So, applying the formula for area of a right-angle triangle given as: - Area = \[\dfrac{1}{2}\times \] base \[\times \] height, we get,
\[\Rightarrow \] Area (OMO’N) = Area (OMO’) + Area (ONO’)
\[\Rightarrow \] Area (OMO’N) = \[\dfrac{1}{2}\times OM\times O'M+\dfrac{1}{2}\times ON\times O'N\]
\[\Rightarrow \] Area (OMO’N) = \[\left( \dfrac{1}{2}\times 7\times 7 \right)+\left( \dfrac{1}{2}\times 7\times 7 \right)\]
\[\Rightarrow \] Area (OMO’N) = 49\[c{{m}^{2}}\] - (1)
Now, we can clearly see the two sectors OMN and O’MN formed. So, applying the formula of a sector of a circle given as: - Area = \[\pi {{r}^{2}}\times \left( \dfrac{\theta }{{{360}^{\circ }}} \right)\], where r = radius of circle, ‘\[\theta \]’ is the angle between the radius, we get,
For sector OMN,
\[\Rightarrow \] OM = ON = r = 7cm
\[\Rightarrow \angle MON=\theta \]
Now, since \[\Delta OMO'\] is an isosceles right – angle triangle with OM = OM’, so \[\angle MOO'=\angle MO'O={{45}^{\circ }}\]. Therefore, we have,
\[\begin{align}
  & \Rightarrow \angle MON=2\angle MOO' \\
 & \Rightarrow \theta =2\times {{45}^{\circ }} \\
 & \Rightarrow \theta ={{90}^{\circ }} \\
\end{align}\]
Similarly, for sector O’MN,
\[\Rightarrow \] O’M = O’N = r = 7cm
\[\Rightarrow \angle MO'N=\theta ={{90}^{\circ }}\]
So, area of sector OMN + area of sector O’MN = \[\pi {{r}^{2}}\times \left( \dfrac{{{90}^{\circ }}}{{{360}^{\circ }}} \right)+\pi {{r}^{2}}\times \left( \dfrac{{{90}^{\circ }}}{{{360}^{\circ }}} \right)\]
\[\Rightarrow \] Area of sector OMN + area of sector O’MN = \[2\pi {{r}^{2}}\times \left( \dfrac{1}{4} \right)\]
\[\Rightarrow \] Area of sector OMN + area of sector O’MN = \[2\pi \times {{7}^{2}}\times \left( \dfrac{1}{4} \right)\]
\[\Rightarrow \] Area of sector OMN + area of sector O’MN = \[\dfrac{49\pi }{2}c{{m}^{2}}\]
Now, the area of the shaded region will be the difference of sum of area of the two sectors and the area of quadrilateral OMO’N. Therefore, we have,
\[\Rightarrow \] Area of shaded region = \[\dfrac{49\pi }{2}-49\]
\[\Rightarrow \] Area of shaded region = \[49\left( \dfrac{\pi }{2}-1 \right)\]
Substituting \[\pi =\dfrac{22}{7}\], we get,
\[\Rightarrow \] Area of shaded region = \[49\left( \dfrac{22}{7\times 2}-1 \right)\]
\[\Rightarrow \] Area of shaded region = \[28c{{m}^{2}}\]
Hence, the area common to both the circles is \[28c{{m}^{2}}\].

Note: One may note that the triangles formed from the quadrilateral, i.e. \[\Delta OMO'\] and \[\Delta ONO'\] are congruent to each other by S – S – S (side – side – side) congruency criteria. This is an important result to remember that “when two circles of the same radius intersect each other then the triangles formed by the line joining the centers of the circles with the points of intersection are congruent to each other”. In many places, this result is used directly. We have substituted \[\pi =\dfrac{22}{7}\] to make our calculation easy.