Question

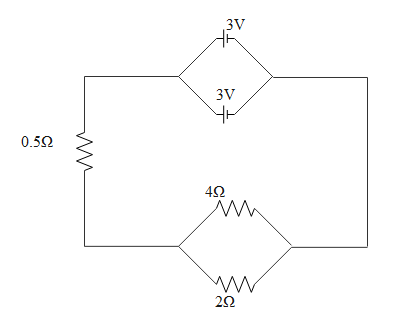
Two cells of 3V each are connected in parallel. An external resistance of $0.5\Omega $ is connected to the junction of two parallel resistors of $4\Omega $ and $2\Omega $ and then to the common terminal of the battery through each resistor as shown in figure. What is the current flowing through the $4\Omega $ resistor?

A. 0.25 A
B. 0.55 A
C. 0.35 A
D. 1.50 A

Answer 1

Hint: In this question, we have to find out the current passing through one resistor. First we should find out the total current passing through the circuit. Then since the resistor is in parallel with the other resistor we should find out the current which is divided to the given resistor.

Formula used:
$\eqalign{
  & {R_s} = {R_1} + {R_2} + {R_3} + ......... \cr
  & \dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....... \cr
  & V = i{R_{eff}} \cr} $

Complete step-by-step answer:
Rate of flow of charge is known as current. A material which allows current to pass through it is known as a conductor. No conductor will be perfect. It will have some resistance. The property to hinder the flow of current is called resistance and a device which does that is known as a resistor.
If the same current is passing through all resistors then we tell those are connected in series. If potential difference is the same for all resistors then those resistors are told to be in parallel.

When resistors are connected in series then effective resistance is ${R_s} = {R_1} + {R_2} + {R_3} + .........$
When resistors are connected in parallel effective resistance will be $\dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + .......$
4 ohms and 2 ohms resistors are in parallel so their effective resistance will be
$\eqalign{
  & \dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \cr
  & \Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{1}{4} + \dfrac{1}{2} \cr
  & \Rightarrow {R_P} = \dfrac{4}{3}\Omega \cr} $
These 4/3 and 0.5 resistors are in series. So total effective will be
$\eqalign{
  & {R_{eff}} = \dfrac{4}{3}\Omega + 0.5\Omega \cr
  & \Rightarrow {R_{eff}} = 1.84\Omega \cr} $
Effective emf due to two parallel cells will be the same as emf of each cell because they are connected in parallel.
$V = i{R_{eff}}$
$\eqalign{
  & \Rightarrow 3 = i\left( {1.84} \right) \cr
  & \Rightarrow i = 1.63A \cr} $
Since 4 ohms and two ohms resistors are in parallel current flowing through each resistor will be inversely proportional to their resistance. Hence current flowing through 4 ohms resistor will be
$\eqalign{
  & {i_4} = \dfrac{2}{{2 + 4}}i \cr
  & \Rightarrow {i_4} = \dfrac{2}{6}i \cr
  & \Rightarrow {i_4} = \dfrac{1}{3}i \cr
  & \Rightarrow {i_4} = \dfrac{1}{3} \times 1.63 \cr
  & \Rightarrow {i_4} = 0.55A \cr} $
Hence 0.55 amperes current will be passed through the 4 ohms resistor.
So, the correct answer is “Option B”.

Note: After finding the total current passing through the circuit we can solve it by another way. That is finding the voltage across the 4 ohms resistor and then applying ohm’s law to find out the current passing through the 4 ohms resistor.