Question

Two cars start out simultaneously from an appointment in the same direction, one of them going at a speed $50kmh^{-1}$ and the other at $40kmh^{-1}$. In half an hour a third car starts from the same point and overtakes the first car in\[1.5h\] after catching up with the second car. The speed of the third car is:
\[\begin{align}
  & A.\text{ }55km{{h}^{-1}} \\
 & B.\text{ }60km{{h}^{-1}} \\
 & C.\text{ }72km{{h}^{-1}} \\
 & D.\text{ }90km{{h}^{-1}} \\
\end{align}\]

Answer 1

Hint: First, we need to calculate the distance travelled by $A$ and $B$ before $C$ started. Then we must equate the distance covered by $C$ when it tries to overtake $B$ and $A$ respectively. Solving the equations, we can find the speed of $C$.

Formula used: distance =speed $\times$ time

Complete step by step solution:
To begin with let us name the first car as $A$ with speed $v_{A}=50km/h$, second car $B$ with speed $v_{B}=40km/h$ and the third car $C$ with speed $v$.
Then, when $C$ starts \[0.5h\] after $A$ and $B$, $A$ and $B$ would have covered a certain distance, the distance covered by $A$ and $B$ is given as, $distance =speed\times time$
Then $d_{A}=v_{A}\times t=50\times 0.5=25km$ and $d_{B}=v_{B}\times t=40\times 0.5=20km$
We can represent the above data on as follows:

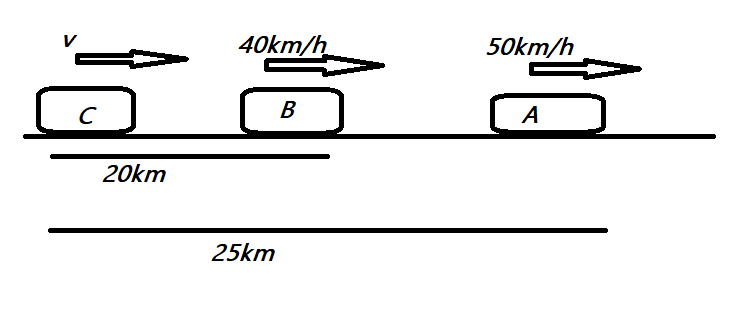
Let us assume that, $C$ overtakes $B$ after $T$ hrs time from when it started, then, the distance covered by $C$ should be equal to the distance covered by $B$,then we can represent this statement mathematically as:
$vT=40T+20$ as the $B$ is still in motion and ahead of $C$ by \[20km\]
Or $T=\dfrac{20}{v-40}$
Also, it is given that $C$ overtakes $A$,\[1.5h\] after catching up with , then we cay ,$C$ overtakes $A$, after $T+1.5$ hrs, then, the distance covered by $C$ should be equal to the distance covered by $A$ then we can represent this statement mathematically as:
$v(T+1.5)=50(T+1.5)+25$ as $A$ is still in motion and ahead of $C$ by \[25km\]
Or $vT=50T+75+25-1.5v$
Or $vT=50T+100-1.5v$
Or$T(v-50)=100-1.5v$
We can substitute for $T$, we get,
Or, $1.5v^{2}-140v+3000=0$
$v=\dfrac{140\pm\sqrt{(-140^{2}-1.5\times 3000)}}{2\times 1.5}$
Solving, we get,$v=60km/h$ or $\dfrac{100}{3}km/h$
To overtake $A$ the speed of $C$ must be greater than the speed of $A$ hence $v=60km/h$

So, the correct answer is “Option B”.

Note: To overtake $A$ and $B$ which started earlier than $C$ the speed of $C$ must be the greatest of all three speeds. Also, for easy calculations, convert all the distances to kilometres and all the time taken to hours as speed is expressed by $km/h$.