Question

Two buildings are in front of each other on either side of a road of width 10 m. From the top of the first building, which is 40 m high, the angle of elevation of the top of the second building is 45 degrees. What is the height of the second building? ​ ​

Answer 1

Hint: To solve this problem, we require the knowledge of basic concepts of trigonometry. We try to understand the diagram in the picture and then use the basic properties of trigonometric angles to solve the problem.

Complete step-by-step answer:
Before solving the problem, we try to understand the basics of trigonometric angles. For a right triangle (ABC),
 

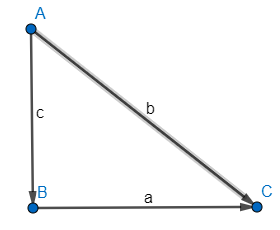
We have sin C = $\dfrac{c}{b}$ , tan C = $\dfrac{c}{a}$ and cos C = $\dfrac{a}{b}$ . Thus, having this information, we come back to the problem in hand, we have the below figure which explains the problem pictorially.

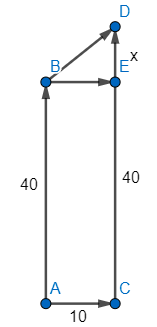
We have a building AB (on the figure) with angle of elevation (angle EBD) of 45 degrees. We need to find the value of x to get the total height of the second building (which will be 40 + x). Now, to solve, we consider the triangle BDE. Since, the angle EBD = 45 degrees, we use tan B = $\dfrac{x}{BE}$ .
Now, $tan {45}^\circ$=1. Thus, we have,
x = BE = AC (Since, by geometry, ACEB is a rectangle and thus AC = BE)
x = BE = AC = 10
Now, since the height of the second building is 40+x, the height is 40 + 10 = 50 m.
Hence, the height of the second building is 50 meters.

Note: In questions involving angle of elevation, most of the times the questions can be solved using trigonometric concepts. In some cases, one may also require the concepts of similarity of triangles to make a complex problem more easy. This type of concept is also useful to find the length of the shadow of a person (with the help of angle of elevation).