Question

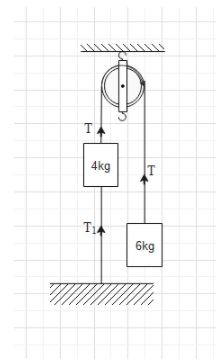
Two bodies of mass 4 and 6 kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string ${{T}_{1}}$ is equal to

A. 19.6 N
B. 25 N
C. 10.6 N
D. 10 N

Answer 1

Hint: Since both the bodies are at rest, the net force on each body will be equal to zero. Therefore, draw the free body diagram of both the bodies and equate the net force to zero. Then using the equations find the value of ${{T}_{1}}$.

Formula used:
F=mg

Complete step-by-step answer:
It is given that the system is at rest. This means that both the bodies are at rest. Therefore, the net force on both the bodies is zero.
Let us draw the free body diagram of both the bodies.
Consider the body of mass 6kg. There are two forces acting on this body. One is the force of gravity exerted by the earth and the other is the tension force. The earth will attract the body towards itself. Hence, the direction of the gravitational force will be downwards. The magnitude of the gravitational force will be mg=6g.
The tension in the string will pull the body upwards. Therefore, the direction of the tension force is upwards.
Therefore, the free body diagram of the 6kg body will look like:

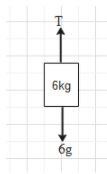
The net force on the body will be ${{F}_{net}}=T-6g$.
However, in this case ${{F}_{net}}=0$. This means that $T-6g=0$.
$\Rightarrow T=6g$ … (i).
Now, consider the body of 4 kg mass.
There are three forces acting on this body. That is the gravitational force (4g) acting downwards, the tension force T pulling it upwards and the tension force ${{T}_{1}}$ pulling it downwards.
Therefore, the free body diagram of this body will be:

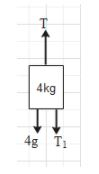
The net force on the body will be ${{F}_{net}}=T-4g-{{T}_{1}}$.
However, in this case ${{F}_{net}}=0$. This means that $T-4g-{{T}_{1}}=0$.
$\Rightarrow {{T}_{1}}=T-4g$
Substitute the value of T from equation (i).
$\Rightarrow {{T}_{1}}=6g-4g=2g$
Let us consider the value of g=$9.8m{{s}^{-2}}$.
Then this implies,
${{T}_{1}}=2g=2(9.8)=19.6N$
This means that the tension ${{T}_{1}}$ is equal to 19.6N.

So, the correct answer is “Option A”.

Note: Note that both bodies are at rest because the 4kg body is attached to the ground with a string. Therefore, the force applied by the 6kg body on the 4kg body is balanced by the tension ${{T}_{1}}$.
Also, note that tension in a stretched string is a pulling force. It acts in both the directions. Meaning, it pulls from the ends.