Question

two bodies begin to fall freely from the same height. The second one begins to fall $\tau s$after the first. The time after which the 1st body begins to fall, the distance between bodies equals $l$ is.
A. $\dfrac{l}{{g\tau }} + \dfrac{\tau }{2}$
B. $\dfrac{{g\tau }}{l} + \tau $
C. $\dfrac{\tau }{{\lg }} + \dfrac{2}{\tau }$
D. $\dfrac{g}{{l\tau }} + \dfrac{\tau }{2}$

Answer 1

Hint:this question is from the kinematics section, so we will be using the kinematics equation $s = ut + \dfrac{1}{2}a{t^2}$ . We have been given two bodies which are at the same height falling freely which means we will take the initial velocity as zero. We will find the distance covered by body $1$ and body $2$ . We will subtract the distance and will put it equal to $l$. Will solve the equation and find our required time.

Complete step by step answer:
Initially it has given that both bodies are at the same height and fall freely.

After $\tau s$ body $1$ will move, and body $2$ would have been moved to $t + \tau $, it is given in the question that after $t + \tau $ the difference between two bodies is $l$ , then we have to find the value of $t$. See the following diagram,

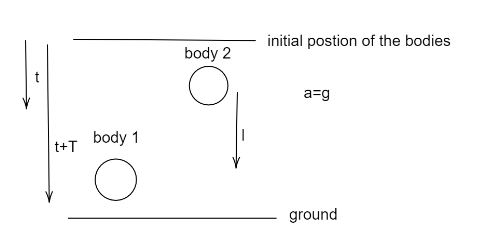
Here $t + T = t + \tau $. We will find the distance covered by body $1$ in time $t + \tau $ and by body $2$ in time $t$ . And by subtracting both and putting it equal to $l$ we will find our required $t$. Using the second equation of motion
$s = ut + \dfrac{1}{2}a{t^2}$
We know $u = 0$ and $a = g$
So, $s = \dfrac{1}{2}g{t^2}$

Let distance covered by body $1$ be ${s_1}$ and distance covered by body $2$ be ${s_2}$
Therefore, ${s_1} = \dfrac{1}{2}g{\left( {t + \tau } \right)^2}$
${s_2} = \dfrac{1}{2}g{t^2}$
Now we have to find the value of $t$
So ${s_2} - {s_1} = l$
Putting values from above
$\dfrac{1}{2}g{t^2} - \dfrac{1}{2}g{\left( {t + \tau } \right)^2} = l$
Solving this we will get
$\dfrac{1}{2}g\left[ {{t^2} - {{\left( {t - \tau } \right)}^2}} \right] = l$
$\Rightarrow \left( {t + t - \tau } \right)\left( {t - t + \tau } \right) = \dfrac{{2l}}{g}$
$\Rightarrow 2t - \tau = \dfrac{{2l}}{{g\tau }}$
$\Rightarrow t = \dfrac{1}{2}\left[ {\dfrac{{2l}}{{g\tau }} + \tau } \right]$
$\therefore t = \dfrac{l}{{g\tau }} + \dfrac{\tau }{2}$

Therefore, option A is the correct answer.

Note:There are two important motion properties that free-falling objects possess:
-Air resistance does not exist for free-falling objects.
-On Earth, all free-falling objects accelerate downwards.
The time measured is from that instant from which the second body was released. Since both the bodies were initially at zero their initial velocity is taken as zero. Acceleration is due to gravity that is why we have taken $a = g$.