Question

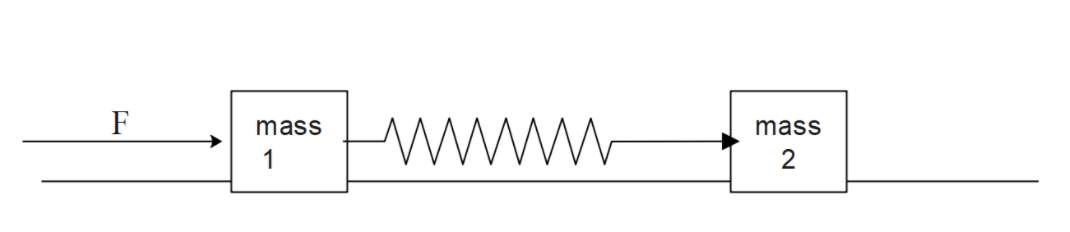
Two blocks of masses ${{m}_{1}}$, ${{m}_{2}}$ are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is $\mu $. Find the minimum constant force F to be applied to ${{m}_{1}}$​ in order to just slide the mass ${{m}_{2}}$ .

Answer 1

Hint: Let us first find the external force acting on the body when force F is applied. Work done by the net external force is calculated. Also, the spring force is calculated in terms of mass and acceleration. Finally, the change in kinetic energy of the total system is zero, work done is equal to the change in kinetic energy, therefore, we can find the force F on mass 1 so that it just slides on mass 2.

Formula used:
$\begin{align}
  & W=\Delta K.E \\
 & W=\int{{{F}^{1}}dx} \\
\end{align}$

Complete step by step answer:
Let us find the net external force acting at any position x,
We know the masses ${{m}_{1}},{{m}_{2}}$, spring constant k,
The force acting is,
$\begin{align}
  & {{F}^{1}}=F-(\mu {{m}_{1}}g+kx) \\
 & \\
\end{align}$
Work done by the net external force in displacing the block m, through a length ${{x}_{0}}$will be,
$\begin{align}
  & {{W}_{ext}}=\int{{{F}^{1}}dx} \\
 & {{W}_{ext}}=\int\limits_{0}^{{{x}_{0}}}{(F-(\mu mg+kx))dx} \\
 & \\
\end{align}$
Also, they spring force required to just move the mass 2 will be,
$\begin{align}
  & k{{x}_{0}}=\mu {{m}_{2}}g \\
 & \Rightarrow {{x}_{0}}=\dfrac{\mu {{m}_{2}}g}{k} \\
\end{align}$as the change in kinetic energy of the system is zero, the work done is equal to change in kinetic energy,
$\begin{align}
  & \Delta K.E=0 \\
 & \Rightarrow W=\Delta K.E \\
 & \Rightarrow F=\mu {{m}_{1}}g+\dfrac{k{{x}_{0}}}{2} \\
 & \therefore F=\mu {{m}_{1}}g+\dfrac{\mu {{m}_{2}}g}{2} \\
\end{align}$
Therefore, we can find the force acted on the mass 1 so that it just slides on mass 2.

Additional Information:
A system of masses connected by springs is a classical system with several degrees of freedom. For example, a system consisting of two masses and three springs has two degrees of freedom. This means that its configuration can be described by two generalized coordinates, which can be chosen to be the displacements of the first and second mass from the equilibrium position.

Note:
Spring material plays an important role in the good functioning of the spring. Materials lie titanium, alloy steel, carbon steel etc. Are really good materials. We may experience spring problems if these springs are susceptible to harsh conditions. We need to coat a spring to prevent it from rusting.