Question

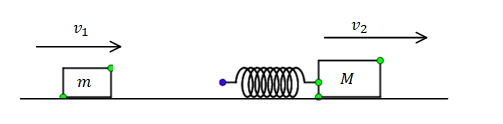
Two blocks of masses m and M are moving with speeds ${v_1}$ and ${v_2}$(${v_1} > {v_2}$) in the same direction on the frictionless surface respectively. M being ahead of m. An ideal spring of force constant k is attached to the backside of M (as shown). The maximum compression of the spring when the block collides is:

A) ${v_1}\sqrt {\dfrac{m}{k}} $.
B) ${v_2}\sqrt {\dfrac{M}{k}} $.
C) $\left( {{v_1} - {v_2}} \right)\sqrt {\dfrac{{mM}}{{\left( {M + m} \right)k}}} $.
D) None of the above is correct.

Answer 1

Hint: The spring energy is the potential energy which is saved by the spring when it is expanded or compressed. The masses m and M will collide as the velocity of the m and is greater than the velocity of the mass M.

Formula used:The formula of the spring energy is given by,
$ \Rightarrow {E_{spring}} = \dfrac{1}{2}k \times {x^2}$
Where the spring constant is k and the length of compression or expansion is x.
The formula of kinetic energy is given by,
$ \Rightarrow K \cdot E = \dfrac{1}{2} \times m \times {v^2}$
Where the mass of the object is m and the velocity is v.

Complete step by step solution:
It is given in the problem that two blocks of masses m and M are moving with speeds ${v_1}$ and ${v_2}$(${v_1} > {v_2}$) in the same direction on the frictionless surface respectively block M being ahead of m an ideal spring of force constant k is attached to the backside of M and we need to find the maximum compression of the spring when the blocks collide.
The initial kinetic energy of the bodies is equal to,
$ \Rightarrow K \cdot {E_1} = \dfrac{1}{2}m{v_1}^2 + \dfrac{1}{2}M{v_2}^2$………eq. (1)
Let v be the velocity of the combined blocks after collision.
Applying the conservation of momentum we get,
$ \Rightarrow m{v_1} + M{v_2} = \left( {M + m} \right) \times v$
$ \Rightarrow v = \dfrac{{m{v_1} + M{v_2}}}{{M + m}}$………eq. (2)
The kinetic energy of the system after collision will be,
$ \Rightarrow K \cdot {E_2} = \dfrac{1}{2} \times m \times {v^2}$
$ \Rightarrow K \cdot {E_2} = \dfrac{1}{2} \times \left( {M + m} \right) \times {v^2}$………eq. (3)
Replacing the value of velocity from the equation (2) into equation (3) we get,
$ \Rightarrow K \cdot {E_2} = \dfrac{1}{2} \times \left( {M + m} \right) \times {v^2}$
$ \Rightarrow K \cdot {E_2} = \dfrac{1}{2} \times \left( {M + m} \right) \times {\left( {\dfrac{{m{v_1} + M{v_2}}}{{M + m}}} \right)^2}$
$ \Rightarrow K \cdot {E_2} = \dfrac{1}{2} \times \dfrac{{{{\left( {m{v_1} + M{v_2}} \right)}^2}}}{{M + m}}$.
The spring energy is given by,
$ \Rightarrow {E_{spring}} = \dfrac{1}{2}k \times {x_{\max .}}^2$
Where the spring constant is k and the length of compression or expansion is x.
The change in kinetic energy is equal to the spring energy,
$ \Rightarrow K \cdot {E_1} - K \cdot {E_2} = {E_{spring}}$
$ \Rightarrow \dfrac{1}{2}m{v_1}^2 + \dfrac{1}{2}M{v_2}^2 - \dfrac{1}{2} \times \dfrac{{{{\left( {m{v_1} + M{v_2}} \right)}^2}}}{{M + m}} = \dfrac{1}{2}k \times {x_{\max .}}^2$
$ \Rightarrow m{v_1}^2 + M{v_2}^2 - \dfrac{{{{\left( {m{v_1} + M{v_2}} \right)}^2}}}{{M + m}} = k \times {x_{\max .}}^2$
$ \Rightarrow \dfrac{{\left( {M + m} \right) \times \left( {m{v_1}^2 + M{v_2}^2} \right) - {{\left( {m{v_1} + M{v_2}} \right)}^2}}}{{M + m}} = k \times {x_{\max .}}^2$
$ \Rightarrow k \times {x_{\max .}}^2 = \dfrac{{\left( {M + m} \right) \times \left( {m{v_1}^2 + M{v_2}^2} \right) - {{\left( {m{v_1} + M{v_2}} \right)}^2}}}{{M + m}}$
\[ \Rightarrow k \times {x_{\max .}}^2 = \dfrac{{Mm{v_1}^2 + {M^2}{v_2}^2 + {m^2}{v_1}^2 + Mm{v_2}^2 - {m^2}{v_1}^2 - {M^2}{v_2}^2 - 2Mm{v_1}{v_2}}}{{M + m}}\]
\[ \Rightarrow k \times {x_{\max .}}^2 = \dfrac{{Mm{v_1}^2 + Mm{v_2}^2 - 2Mm{v_1}{v_2}}}{{M + m}}\]
\[ \Rightarrow k \times {x_{\max .}}^2 = Mm \times \left( {\dfrac{{{v_1}^2 + {v_2}^2 - 2{v_1}{v_2}}}{{M + m}}} \right)\]
\[ \Rightarrow k \times {x_{\max .}}^2 = \dfrac{{Mm}}{{M + m}} \times \left( {{v_1}^2 + {v_2}^2 - 2{v_1}{v_2}} \right)\]
\[ \Rightarrow k \times {x_{\max .}}^2 = \dfrac{{Mm}}{{M + m}} \times {\left( {{v_1} - {v_2}} \right)^2}\]
\[ \Rightarrow {x_{\max .}}^2 = \dfrac{{Mm}}{{k\left( {M + m} \right)}} \times {\left( {{v_1} - {v_2}} \right)^2}\]
\[ \Rightarrow {x_{\max .}} = \left( {{v_1} - {v_2}} \right) \times \sqrt {\dfrac{{Mm}}{{k\left( {M + m} \right)}}} \].
The maximum compression of the spring is equal to \[{x_{\max .}} = \left( {{v_1} - {v_2}} \right) \times \sqrt {\dfrac{{Mm}}{{k\left( {M + m} \right)}}} \].

The correct answer for this problem is option C.

Note: The linear conservation of momentum says that the total energy of the blocks before and after the collision will be conserved. It is advised to the students to understand and remember the formula of the momentum and also the formula of the spring energy as it is very useful in solving problems like these.