Question

Two blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of $7m/s$ to the heavier block in the direction of the lighter block. The velocity of the center of mass is
\[
  A.{\text{ }}4m/s \\
  B.{\text{ }}5m/s \\
  C.{\text{ }}10m/s \\
  D.{\text{ }}3m/s \\
 \]

Answer 1

Hint: In order to solve this problem we will use the formula for the velocity of the center of mass of two masses with the help of the values provided in the problem. We will use the velocity of the second mass as zero as no impulse is provided to the second block.
Formula used- ${V_{cm}} = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}}$

Complete step-by-step solution:

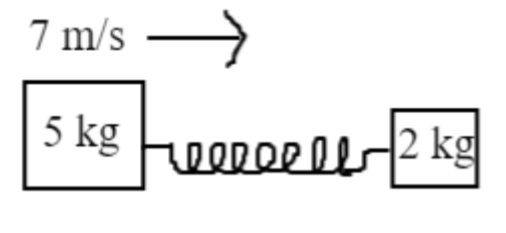
Given that two blocks of masses 5kg and 2kg.
Let ${m_1} = 5kg$
And ${m_2} = 2kg$
Given that impulse is provided to first block
So, ${v_1} = 7m/s$
Here light block of 2kg is at rest so the velocity of second block will be zero
So ${v_2} = 0m/s$
We know that velocity of the centre of mass is given as
${V_{cm}} = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}}$
Substitute all the given values in above formula, we get
\[
  \because {V_{cm}} = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}} \\
   \Rightarrow {V_{cm}} = \dfrac{{5 \times 7 + 2 \times 0}}{{5 + 2}} \\
   \Rightarrow {V_{cm}} = \dfrac{{35}}{7} \\
   \Rightarrow {V_{cm}} = 5m/s \\
 \]
Hence, the velocity of the centre of mass is \[5m/s\]
So, the correct answer is option B.

Note: The center of mass of a mass distribution in space is the particular point where the relative weighted position of the distributed mass sums is at zero. This is the point at which a force can be applied without an angular acceleration to cause linear acceleration. The center of mass is a useful reference point for calculations in mechanics involving spatially distributed masses, such as the planetary bodies' linear and angular momentum and rigid body dynamics.