Question

Two blocks of masses $ 2kg $ and $ 4kg $ are hanging with the help of a massless string passing over an ideal pulley inside an elevator. The elevator is moving upward with an accelerating $ \dfrac{g}{2} $ . The tension in the string connected between the blocks will be (take $ g = 10m/{s^2} $ )
(A) $ 40N $
(B) $ 60N $
(C) $ 80N $
(D) $ 20N $

Answer 1

Hint: The force on a body is directly proportional to the rate of change of momentum. There is an equal and opposite action for every action. Due to the inertia, the force on the object is having an opposite force In the opposite direction.

Complete Step By Step Answer:
The frame of reference of the lift’s inside, which is attached to the floor, is moving upwards with an acceleration of $ \dfrac{g}{2} $ . So for applying Newton's laws, we need to add a pseudo force $ \left( { = mass \times \dfrac{g}{2}} \right) $ in the downward direction for each mass. In other words, we can say the effective downwards.

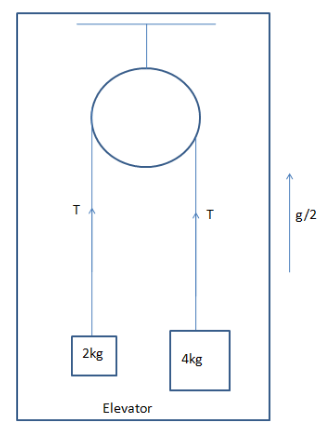
The $ {M_1} $ is the $ 4kg $ mass that is heavier and accelerates downwards. Here, $ {M_2} $ is the $ 2kg $ mass it moves upwards with the equal acceleration of $ {M_1} $ . Let us consider the tight string which has even tension $ T $ throughout the string $ g' = g + \dfrac{g}{2} = \dfrac{{3g}}{2} $
 $ \Rightarrow 4\left( {g + \dfrac{g}{2}} \right) - T = 4a $ ………..(1)
 $ \Rightarrow T - 2\left( {g + \dfrac{g}{2}} \right) = 2a $ ……….(2)
Here,
 $ T - 3g = 2a $
Now rearranging the equation,
 $ T = 3g + 2a $
Now solving the equation (1) from equation (2)
 $ \Rightarrow 4\left( {g + \dfrac{g}{2}} \right) - \left( {3g + 2a} \right) = 4a $
After simplification,
 $ a = \dfrac{g}{2} $
Now apply the values in the equation we get
Hence,
 $ T = 3g + 2\left( {\dfrac{g}{2}} \right)t $
After solving the equation we get,
 $ T = 40N $
Finally, the answer is an option (A).

Note:
There are three laws that will help to describe the relationship between the object's motion and force on an object.
When an object moves from one place to another which is called a motion,
A force that makes an object with a heavy mass can change its velocity; it includes beginning moving from a state of rest.