Question

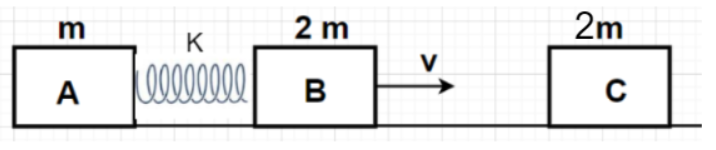
Two blocks A and B of masses m and 2m, respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block B collides head-on with a third block C of mass 2m, at rest, the collision is completely inelastic. Calculate the maximum compression of the spring.

Answer 1

Hint- Here, we will proceed by finding the initial velocity of centre of mass of the complete system. Then, we will apply linear momentum conservation on the system consisting of blocks B and C. Then, we will apply energy conservation to the complete system.

Complete step-by-step solution -
Formulas Used: ${{\text{v}}_0} = \dfrac{{{{\text{m}}_1}{{\text{v}}_1} + {{\text{m}}_2}{{\text{v}}_2} + {{\text{m}}_3}{{\text{v}}_3}}}{{{{\text{m}}_1} + {{\text{m}}_2} + {{\text{m}}_3}}}$, KE = $\dfrac{1}{2}{\text{m}}{{\text{v}}^2}$ and PE = $\dfrac{1}{2}{\text{k}}{{\text{x}}^2}$.
Given, Mass of block A = m
Mass of block B = 2m
Mass of block C = 2m
Initial velocity of block A = v
Initial velocity of block B = v
Initial velocity of block C = 0
Force constant of spring = k
As we know that if we have three bodies A, B and C of masses ${{\text{m}}_1}{\text{,}}{{\text{m}}_2}$ and ${{\text{m}}_3}$ respectively and having velocities ${{\text{v}}_1}{\text{,}}{{\text{v}}_2}$ and ${{\text{v}}_3}$ respectively, then
Velocity of centre of mass of this system (consisting of all these three masses), ${{\text{v}}_0} = \dfrac{{{{\text{m}}_1}{{\text{v}}_1} + {{\text{m}}_2}{{\text{v}}_2} + {{\text{m}}_3}{{\text{v}}_3}}}{{{{\text{m}}_1} + {{\text{m}}_2} + {{\text{m}}_3}}}$
Using the above formula for the given system, we can write
Initial velocity of centre of mass of complete system, \[{{\text{v}}_0} = \dfrac{{{\text{mv}} + 2{\text{mv}} + 2{\text{m}}\left( 0 \right)}}{{{\text{m}} + 2{\text{m}} + 2{\text{m}}}} = \dfrac{{{\text{3mv}}}}{{5{\text{m}}}} = \dfrac{{{\text{3v}}}}{5}\]
It is given that complete inelastic collision is occurring between blocks B and C which will lead to sticking of blocks B and C together (i.e., after collision blocks B and C will be moving with the same velocity). Let the final velocity of block B which is equal to the final velocity of block C be ${{\text{v}}_1}$.
Let us suppose the maximum compression obtained in the spring after the collision be x
Since, the linear momentum (which is equal to the product of mass and velocity) remains same after collision takes place
Consider blocks B and C as a whole system and applying linear momentum conservation, we get
Total linear momentum of blocks B and C before collision = Total linear momentum of blocks B and C after collision
$ \Rightarrow $ (Mass of block B)(Initial velocity of block B) = (Mass of block B)(Final velocity of block B) + (Mass of block C)(Final velocity of block C)
$
   \Rightarrow \left( {{\text{2m}}} \right)\left( {\text{v}} \right) = \left( {2{\text{m}}} \right)\left( {{{\text{v}}_1}} \right) + \left( {2{\text{m}}} \right)\left( {{{\text{v}}_1}} \right) \\
   \Rightarrow 2{\text{mv}} = 2{\text{m}}{{\text{v}}_1} + 2{\text{m}}{{\text{v}}_1} \\
   \Rightarrow 4{\text{m}}{{\text{v}}_1} = 2{\text{mv}} \\
   \Rightarrow {{\text{v}}_1} = \dfrac{{2{\text{mv}}}}{{4{\text{m}}}} \\
   \Rightarrow {{\text{v}}_1} = \dfrac{{\text{v}}}{2} \\
 $
Final velocity of block B = Final velocity of block C = ${{\text{v}}_1} = \dfrac{{\text{v}}}{2}$
After collision, block A is moving with initial velocity only i.e., v.
Since, kinetic energy of body having mass m and velocity v is given by KE = $\dfrac{1}{2}{\text{m}}{{\text{v}}^2}$
Also, potential energy of spring having force constant k and compression x is given by PE = $\dfrac{1}{2}{\text{k}}{{\text{x}}^2}$
According to Energy conservation, we can write
Total kinetic energy before collision + Potential energy developed in the spring due to compression
= Total kinetic energy after collision
 $ \Rightarrow $ (Total mass of complete system)( Initial velocity of centre of mass of complete system) + Potential energy developed in the spring due to compression = Kinetic energy of block A + Kinetic equation of block B + Kinetic equation of block C
 \[
   \Rightarrow \dfrac{1}{2}\left( {{\text{m}} + {\text{2m}} + {\text{2m}}} \right){{\text{v}}_0}^2 + \dfrac{1}{2}{\text{k}}{{\text{x}}^2} = \dfrac{1}{2}{\text{m}}{{\text{v}}^2} + \dfrac{1}{2}\left( {{\text{2m}}} \right){{\text{v}}_1}^2 + \dfrac{1}{2}\left( {{\text{2m}}} \right){{\text{v}}_1}^2 \\
   \Rightarrow \dfrac{{5{\text{m}}{{\text{v}}_0}^2}}{2} + \dfrac{1}{2}{\text{k}}{{\text{x}}^2} = \dfrac{{{\text{m}}{{\text{v}}^2}}}{2} + {\text{m}}{{\text{v}}_1}^2 + {\text{m}}{{\text{v}}_1}^2 \\
   \Rightarrow \dfrac{{5{\text{m}}{{\text{v}}_0}^2}}{2} + \dfrac{1}{2}{\text{k}}{{\text{x}}^2} = \dfrac{{{\text{m}}{{\text{v}}^2}}}{2} + 2{\text{m}}{{\text{v}}_1}^2 \\
   \Rightarrow \dfrac{1}{2}{\text{k}}{{\text{x}}^2} = \dfrac{{{\text{m}}{{\text{v}}^2}}}{2} - \dfrac{{5{\text{m}}{{\text{v}}_0}^2}}{2} + 2{\text{m}}{{\text{v}}_1}^2 \\
   \Rightarrow {{\text{x}}^2} = \dfrac{2}{{\text{k}}}\left[ {\dfrac{{{\text{m}}{{\text{v}}^2}}}{2} - \dfrac{{5{\text{m}}{{\text{v}}_0}^2}}{2} + 2{\text{m}}{{\text{v}}_1}^2} \right] \\
   \Rightarrow {{\text{x}}^2} = \dfrac{1}{{\text{k}}}\left( {{\text{m}}{{\text{v}}^2} - 5{\text{m}}{{\text{v}}_0}^2 + 4{\text{m}}{{\text{v}}_1}^2} \right) \\
   \Rightarrow {{\text{x}}^2} = \dfrac{{\text{m}}}{{\text{k}}}\left( {{{\text{v}}^2} - 5{{\text{v}}_0}^2 + 4{{\text{v}}_1}^2} \right) \\
 \]
By substituting \[{{\text{v}}_0} = \dfrac{{{\text{3v}}}}{5}\] and ${{\text{v}}_1} = \dfrac{{\text{v}}}{2}$ in the above equation, we get
\[
   \Rightarrow {{\text{x}}^2} = \dfrac{{\text{m}}}{{\text{k}}}\left[ {{{\text{v}}^2} - 5{{\left( {\dfrac{{{\text{3v}}}}{5}} \right)}^2} + 4{{\left( {\dfrac{{\text{v}}}{2}} \right)}^2}} \right] \\
   \Rightarrow {{\text{x}}^2} = \dfrac{{\text{m}}}{{\text{k}}}\left[ {{{\text{v}}^2} - 5\left( {\dfrac{{{\text{9}}{{\text{v}}^2}}}{{25}}} \right) + 4\left( {\dfrac{{{{\text{v}}^2}}}{4}} \right)} \right] \\
   \Rightarrow {{\text{x}}^2} = \dfrac{{\text{m}}}{{\text{k}}}\left[ {{{\text{v}}^2} - \dfrac{{{\text{9}}{{\text{v}}^2}}}{5} + {{\text{v}}^2}} \right] \\
   \Rightarrow {{\text{x}}^2} = \dfrac{{\text{m}}}{{\text{k}}}\left[ {{\text{2}}{{\text{v}}^2} - \dfrac{{{\text{9}}{{\text{v}}^2}}}{5}} \right] \\
   \Rightarrow {{\text{x}}^2} = \dfrac{{\text{m}}}{{\text{k}}}\left[ {\dfrac{{10{{\text{v}}^2} - 9{{\text{v}}^2}}}{5}} \right] \\
   \Rightarrow {{\text{x}}^2} = \dfrac{{\text{m}}}{{\text{k}}}\left[ {\dfrac{{{{\text{v}}^2}}}{5}} \right] \\
   \Rightarrow {{\text{x}}^2} = \dfrac{{{\text{m}}{{\text{v}}^2}}}{{{\text{5k}}}} \\
   \Rightarrow {\text{x}} = \sqrt {\dfrac{{{\text{m}}{{\text{v}}^2}}}{{{\text{5k}}}}} \\
 \]
Therefore, the maximum compression of the spring will be \[\sqrt {\dfrac{{{\text{m}}{{\text{v}}^2}}}{{{\text{5k}}}}} \].

Note- In this particular problem, while writing linear momentum conversation between blocks B and C, the linear momentum due to block C before collision is neglected because initially, the block C is at rest (i.e., its velocity is zero) and hence, its contribution for the linear momentum before collision will be zero.