Question

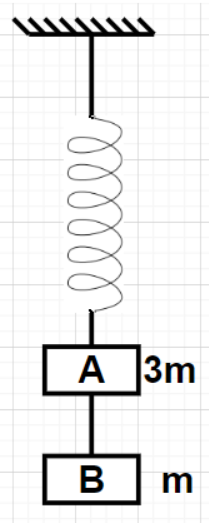
Two blocks A and B of masses 3m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. What are the magnitudes of acceleration of A and B immediately after the string is cut respectively?
${\text{A}}{\text{.}}$ \[\dfrac{{\text{g}}}{3}\], g
${\text{B}}{\text{.}}$ g, g
${\text{C}}{\text{.}}$ \[\dfrac{{\text{g}}}{3}\], \[\dfrac{{\text{g}}}{3}\]
${\text{D}}{\text{.}}$ g, \[\dfrac{{\text{g}}}{3}\]

Answer 1

Hint: Here, we will proceed by drawing the free body diagrams for block A and B before and after the string is cut. Then, in the first case we will apply laws of equilibrium and in the latter case, we will apply Newton’s second law of motion.
Formulas Used: Weight = (Mass of the body)(g) and Force = (Mass)(Acceleration).

Complete Step-by-Step solution:

Given, Mass of block A = 3m
Mass of block B = m
Let the accelerations of block A and B immediately after the string is cut be a and b respectively. Let T be the tension in the string, S be the spring force acting on block A
As we know that the weight (or gravitational force acting downwards) of body having mass m will be equal to mg where g is the acceleration due to gravity
Weight of block A (acting in downward direction) = 3mg
Weight of block B (acting in downward direction) = mg
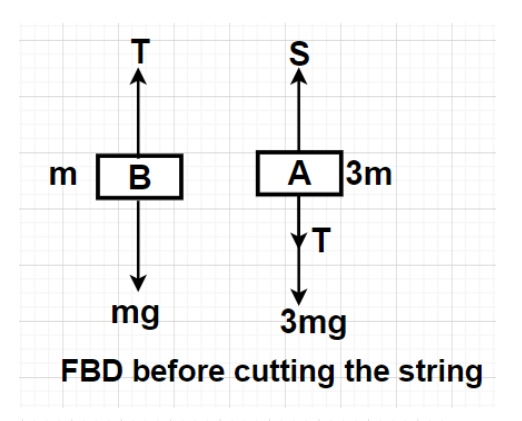
Case I: Before the cutting of the string
Equilibrium will be established in the system and the various forces acting on the blocks A and B are shown in the free body diagram (FBD).
At equilibrium, the sum of all the upward forces acting on a body will be equal to the sum of all the downwards forces acting on the same.
For block A, S = T+3mg $ \to (1)$
For block B, T = mg
By substituting T = mg in equation (1), we get
S = mg+3mg = 4mg
Now, cut the string connecting blocks A and B.
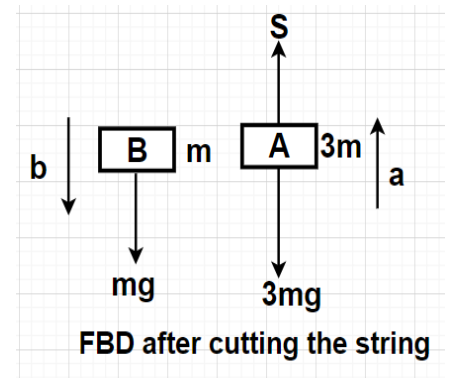
Case II: After the cutting of the string
Both the blocks will possess some accelerations. The free body diagram (FBD) for this case is also drawn which tells us about the various forces acting on the blocks.
According to Newton’s second law of motion, the external force F acting on a body having mass m and acceleration a is given by F = ma
Using Newton’s second law of motion for block B, we have
mg = mb
$ \Rightarrow $b = g
Using Newton’s second law of motion for block A, we have
S – 3mg = 3ma
By substituting S = 4mg in the above equation, we get
$ \Rightarrow $4mg – 3mg = 3ma
$ \Rightarrow $3ma = mg
$ \Rightarrow {\text{a}} = \dfrac{{{\text{mg}}}}{{3{\text{m}}}} = \dfrac{{\text{g}}}{3}$
Therefore, the magnitudes of acceleration of blocks A and B immediately after the string is cut are $\dfrac{{\text{g}}}{3}$ (in upward direction) and g (in downward direction) respectively.
Hence, option C is correct.

Note- In this particular problem, we have assumed the directions of accelerations a and b as upwards and downwards respectively as shown in FBD. If we would have assumed their directions to be opposite, then negative signs would have occurred. After the string is cut, tension force T is removed and accelerations are imparted to the blocks.