Question

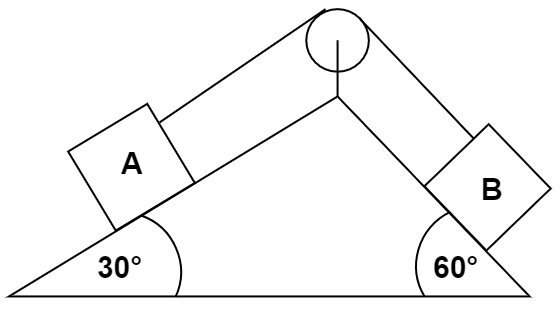
Two blocks \[A\] and \[B\] of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in the figure. Find the magnitude of acceleration of the centre of mass of the two blocks when they are released from rest. Neglect friction.

Answer 1

Hint: The acceleration of the centre of the mass of this particular system is calculated by using the vector equation of the acceleration of the two masses. The vector equation of both the blocks, that is, block \[A\] and the vector equation of the block \[B\] is used to find out the magnitude of the required acceleration of the centre of mass.

Complete step by step answer:
Here, we are given that, the block \[A\] and the block \[B\], are having the same mass $m$,the block \[A\] is sliding at an angle of inclination of ${30^ \circ }$ whereas the block \[B\] is sliding at an angle of inclination of ${60^ \circ }$. Now, we know that the force is the product of the mass of the object and the acceleration of the object.

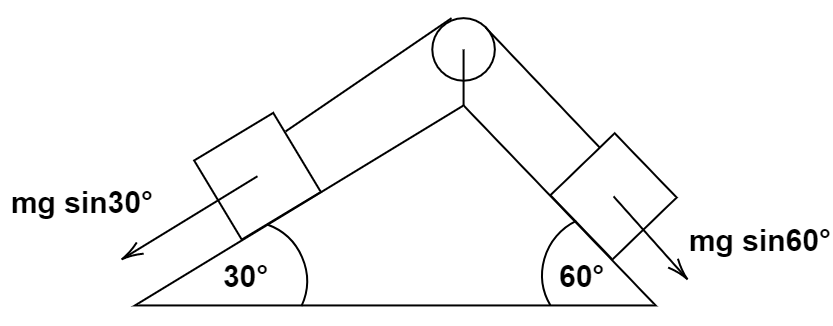
Let us consider the inclination, which is given to us, with respect to the x axis. So, the acceleration of the two mass in the vector form comes out to be,
The vector equation for the acceleration of the block \[A\] is,
$\overrightarrow {{a_A}} = mg\sin {30^ \circ }\widehat i$
Similarly, the vector equation for the acceleration of the block \[B\] is,
$\overrightarrow {{a_B}} = mg\sin {60^ \circ }\widehat j$
Now, the acceleration of the centre of mass is,
${\overrightarrow a _{cm}} = \dfrac{{mg\sin {{30}^ \circ }\widehat i + mg\sin {{60}^ \circ }\widehat j}}{{{m_A} + {m_B}}}$
Since, the mass of both the blocks are same. So, the above equation can be written as,
${\overrightarrow a _{cm}} = \dfrac{{mg\sin {{30}^ \circ }\widehat i + mg\sin {{60}^ \circ }\widehat j}}{{m + m}}$
${\overrightarrow a _{cm}} = \dfrac{{mg\sin {{30}^ \circ }\widehat i + mg\sin {{60}^ \circ }\widehat j}}{{2m}}$
On putting the value of the trigonometric functions, we get,
${\overrightarrow a _{cm}} = \dfrac{{mg\left( {\dfrac{1}{2}} \right)\widehat i + mg\left( {\dfrac{{\sqrt 3 }}{2}} \right)\widehat j}}{{2m}}$
On taking common terms,
${\overrightarrow a _{cm}} = \dfrac{{mg}}{{4m}}\left( {\widehat i + \sqrt 3 \widehat j} \right)$
${\overrightarrow a _{cm}} = \dfrac{g}{4}\left( {\widehat i + \sqrt 3 \widehat j} \right)$
Now, we need to change this vector equation in terms of magnitude. So,
${\overrightarrow a _{cm}} = \dfrac{g}{4}\sqrt {{{\left( 1 \right)}^2} + {{\left( {\sqrt 3 } \right)}^2}} $
${\overrightarrow a _{cm}} = \dfrac{g}{4}\sqrt {1 + 3} $
On further simplifying this, we get,
\[{\overrightarrow a _{cm}} = \dfrac{g}{4}\sqrt 4 \]
\[{\overrightarrow a _{cm}} = \dfrac{g}{4} \times 2\]
On dividing numerator and denominator, we get,
\[{\overrightarrow a _{cm}} = \dfrac{g}{2}\]
Therefore, the value of the acceleration of the centre of mass is \[{\overrightarrow a _{cm}} = \dfrac{g}{2}\].

Note: It is important to note that in this question, the two blocks are sliding in the inclined plane, so the acceleration of the centre of the mass of the system is determined by using the various trigonometric functions. While using the trigonometric function, the students must carefully solve the first step as it is used to find the acceleration of the centre of the mass.