Question

Two blocks A and B having masses ${m_1} = 1kg$, ${m_2} = 4kg$ are arranged as shown in figure. The pulleys P and Q are light, and frictionless. All the blocks are resting on a horizontal floor and the pulleys are held such that the string remains just taut. At moment $t = 0$ a force $F = 30t(N)$ starts acting on the pulley P along. Vertically upward direction as shown in the pulley P along vertically upward direction as shown in figure. Calculate

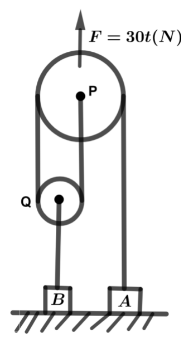
(i) The time when the blocks A and B lose contact with ground.
(ii) The velocity of A and B loses contact with ground.
(iii) The height raised by A upto this instant.
(iv) The work done by the force F upto this instan.

Answer 1

Hint:Given in the question two blocks A and B having masses. When they are attached to some pulleys P and Q then there is applied some force on A and B here given force. Force is acting on the pulley P along in vertically upward direction. For calculating they have given some points we have to prove.

Complete step by step answer:
(i) For calculating the above given conditions, where tension acts $T$ in upward direction and tension acts $2T$ in downward direction. Now we are going to solve the first condition, Time when two blocks A and B lose contact with ground.First we are calculating the time in block A. Here tension, $T = 10N$
And force $F = 3T$
Given data $F = 30t$
That means, $30t = 3 \times 10$
Where time in block A is, $t = 1\sec $
Now time in block B,
Here B losses contact that means,
$2T = 40$
$\Rightarrow T = 20N$
So here, $F = 3T$
That means,
$30t = 3 \times 20 \\
\Rightarrow 30t = 60 \\
\therefore t = 2\sec $

(ii) We have proved the time when blocks A and B lose contact with ground.
In second case we are going to calculate the velocity of A and B
$T - 10 = a$
So here $3T = F = 30t$
Already we have written in case one,
So here applying integration part to the velocity from $0$ to $v$ that means,
$V = \int\limits_0^v {dv} \\
\Rightarrow V = 10\int\limits_1^2 {\left( {t - 1} \right)dt} \\ $
As we known $\int {dx = x} $ so here, by applying integration values we get,
$V = 10\left( {\dfrac{{2 - 1}}{2}} \right) \\
\Rightarrow V = \dfrac{{10}}{2} \\
\therefore V = 5\,m{s^{ - 1}} \\ $
Velocity of value, $V = 5\,m{s^{ - 1}}$

(iii) Now we are discussing the condition for third part, here height A is raised up to instant,
For this we are using integration part,
$\int {dx = \int\limits_1^2 {5{t^2} - 10t + 5dt} } $
Here $\int {dx = \int\limits_a^b {f(x)dx = } \dfrac{{{x^2}}}{{a + b}}} $, by applying the values of integration part, we get
$x = {\left[ {\dfrac{{5{t^3}}}{3} - 5{t^2} + 5t} \right]_1}^2 \\
\therefore x = \dfrac{5}{3}\left( {8 - 1} \right) - 5\left( {4 - 1} \right) + 5 \\ $
By solving above we get height raise is up to $x = \dfrac{5}{3}\,m$

(iv) In fourth part, work done by force is,
$W = \int {Fdx} $
$\Rightarrow W = \int {30tdx} \\
\Rightarrow W = \int {30t\left[ {\dfrac{{10{t^2}}}{6} - \dfrac{{10t}}{3} + \dfrac{{10}}{6}} \right]} dt \\ $
Now we are applying integrals from $1$ to $2$ in time t,
Therefore, $W = \int\limits_1^2 {\dfrac{{300}}{6}{t^3} - \dfrac{{300}}{3}{t^2} + \dfrac{{300}}{6}tdt} $
$\therefore W = {\left[ {\dfrac{{50{t^4}}}{4} - \dfrac{{100{t^3}}}{3} + 25{t^2}} \right]^2}_1$
By adding those values we get total work done, $W = \dfrac{{175}}{6}\,J$.

Note:In the solution part we discussed all the four conditions and we have proved all of them. For the first condition we have proved time is constant and in the second condition we have proved the velocity value by using integration from time $t = 1$ to $t = 2$. In the third case we have proved the height is raised up to its instant and in fourth condition we have proved the total work done by the force upto its instant.