Question

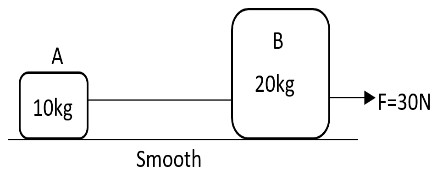
Two blocks A and B are connected by a massless string as represented in the diagram. A force of $30N$ is applied on block B, the distance travelled by centre of mass in $2s$ starting from the rest will be

$\begin{align}
  & A.1m \\
 & B.2m \\
 & C.3m \\
 & D.\text{none of these} \\
\end{align}$

Answer 1

Hint: First of all find the total mass of the centre of masses. Draw the free body diagram of the centre of mass of the system. Calculate the force acting on the centre of mass. Using this, find the acceleration of the centre of mass. Then use the second law of motion for calculating the displacement. This all will help you in solving this question.

Complete answer:
First of all, the mass of the block A is given as,
${{m}_{A}}=10kg$
Mass of the block B has been mentioned as,
${{m}_{B}}=20kg$
Time taken has been mentioned as,
$t=2s$
Force acting can be written as,
$F=30N$
Let us assume that the initial velocity on the body be,
$u=0m{{s}^{-1}}$
The total mass on the centre of mass will be,
$M={{m}_{A}}+{{m}_{B}}$
Substituting the values in it,
$\Rightarrow M=10+20=30kg$
The force acting on it will be equivalent to the force acting on the centre of mass. That is,
$\Rightarrow F=30N$
The free body diagram of the centre of mass can be shown as,

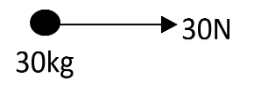
It is to be noted that the internal tension will not affect the centre of mass motion.
The acceleration of the centre of mass is mentioned as,
$a=\dfrac{F}{M}$
Substituting the values in it,
$\Rightarrow a=\dfrac{30}{30}=1m{{s}^{-2}}$
According to the second equation of motion,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
Substitute the values in it will give,
$\Rightarrow s=\dfrac{1}{2}\times 1\times {{2}^{2}}=2m$

So, the correct answer is “Option B”.

Note:
The centre of mass is defined as the position described which is relative to an object or system of bodies. It will be the mean position of all the portions of the system which will be weighted in accordance with their masses. In short the centre of mass is a point where the whole mass of the system is assumed to be concentrated.