Question

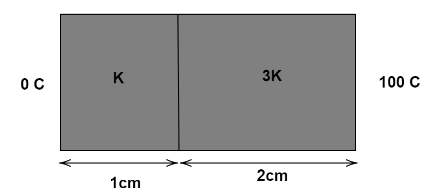
Two bars of thermal conductivities \[K\] and \[3K\] and lengths \[1{\text{ cm}}\] and \[{\text{2 cm}}\] respectively have equal cross-sectional area. They are joined lengthwise as shown in the figure. If the temperature of the ends of the composite bar is \[{0^ \circ }C\] and \[{100^ \circ }C\] respectively (see figure), then the temperature of the interface \[\left( \varphi \right)\] is
A. \[{50^ \circ }C\]
B. \[{\dfrac{{100}}{3}^ \circ }C\]
C. \[{60^ \circ }C\]
D. \[{\dfrac{{200}}{3}^ \circ }C\]

Answer 1

Hint:In this question, we need to find the temperature of the interface of two composite slabs. As they are connected in series the heat current through both the slabs must be equal. Assume the temperature as \[{T^ \circ }C\] and write the heat current for both slabs and equate them as they must be equal. On solving, we get the temperature of interface

Formula used:
\[H = \dfrac{{dQ}}{{dt}} = - KA\dfrac{{dT}}{{dx}} = KA\dfrac{{\left( {{T_1} - {T_2}} \right)}}{l}\]
Where \[H\] is the heat current, \[K\] is the thermal conductivity, \[dT\] is the temperature difference and \[l\] is the length of the slab.

Complete step by step answer:
We are given two bars of thermal conductivities \[K\] and \[3K\].
The Length of the first bar is, \[{l_1} = 1{\text{ }}cm\]
The Length of the second bar is, \[{l_2} = 2{\text{ }}cm\]
The Area of cross-section of both the bars is \[A\]
\[{T_1} = {0^ \circ }C\]
\[\Rightarrow {T_2} = {100^ \circ }C\]
Let the temperature of the interface be \[{T^ \circ }C\]
Heat current through the first composite slab,
\[H = KA\dfrac{{\left( {{T_1} - T} \right)}}{1}\]
Heat current through the second composite slab,
\[H = 3KA\dfrac{{\left( {T - {T_2}} \right)}}{2}\]

But heat current through both the slabs must be equal. Therefore,
\[KA\dfrac{{\left( {{T_1} - T} \right)}}{1} = 3KA\dfrac{{\left( {T - {T_2}} \right)}}{2}\]
Dividing both sides by \[KA\] we get,
\[ \Rightarrow {T_1} - T = \dfrac{3}{2}\left( {T - {T_2}} \right)\]
Substituting \[{T_1} = {0^ \circ }C\] and \[{T_2} = {100^ \circ }C\] we get,
\[ \Rightarrow - T = \dfrac{3}{2}\left( {T - 100} \right)\]
\[ \Rightarrow \dfrac{5}{2}T = 150\]
\[ \therefore T = {60^ \circ }C\]
Hence, the temperature of the interference of the two composite blocks is\[{60^ \circ }C\].

Therefore, the correct option is C.

Note: The negative signed use is \[H = \dfrac{{dQ}}{{dt}} = - KA\dfrac{{dT}}{{dx}}\] is used to make \[\dfrac{{dQ}}{{dt}}\] a positive quantity since \[\dfrac{{dT}}{{dx}}\] is a negative quantity. The constant \[K\] , called thermal conductivity, is the measure of the ability of the material to conduct heat. A substance with a large value of \[K\] means it is a good conductor of heat. The value of \[K\] depends on temperature but can be taken practically constant if the temperature difference between the two ends of the substance is not too great.