Question

Two balls of mass 1 kg and 2 kg respectively are connected to the two ends of the spring. The two balls are pressed together and placed on a smooth table. When released, the lighter ball moves with an acceleration of$2m{s^{ - 2}}$. The acceleration of the heavier ball will be:
A) $0.2m{s^{ - 2}}$
B) $1m{s^{ - 1}}$
C) $2m{s^{ - 2}}$
D) $4m{s^{ - 2}}$

Answer 1

Hint: The force applied by spring on the ball of mass 1 kg is equal to the force applied by the spring on the ball of mass 2 kg. The force applied by spring is equal to$F = - k \cdot x$, where $k$ is the spring constant and $x$ is the compression. Let accelerations of 1 kg mass be ${a_1}$ and acceleration of mass 2 kg be ${a_2}$.

Complete step by step solution:
Let the acceleration of the ball of mass 1 kg be ${a_1}$ and acceleration of the ball of mass 2 kg be ${a_2}$.
Diagram of the given condition,

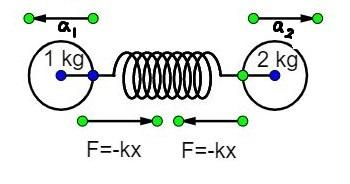
Step 2:
The force applied by the spring on the ball of mass 2 kg is $F = - k \cdot x$, and the same force was applied by the spring on the ball of mass 1 kg.
Step 3:
Let the acceleration of the mass 1 kg be ${a_1}$ and the acceleration of the mass 2 kg be ${a_2}$. As the force applied by the spring on both the masses are the same and force is also given as $F = m \cdot a$.
Therefore,
$ - k \cdot x = m \cdot {a_1}$
For body of mass 1 kg the acceleration is ${a_1}$,
$
   - k \cdot x = 1 \cdot {a_1} \\
   - k \cdot x = {a_1} \\
 $………eq.(1)
For body of mass 2 kg the acceleration of body is ${a_2}$,
$
   - k \cdot x = 2 \cdot {a_2} \\
   - k \cdot x = 2{a_2} \\
 $………eq.(2)
Dividing equation (1) from (2) we get,
\[
  \dfrac{{ - k \cdot x}}{{ - k \cdot x}} = \dfrac{{{a_1}}}{{2{a_2}}} \\
  1 = \dfrac{{{a_1}}}{{2{a_2}}} \\
  {a_1} = 2{a_2} \\
 \]
As it is given that the acceleration of the 1 kg ball is $2m{s^{ - 2}}$, we can put the value $a$ in the above equation and get the acceleration of the ball of mass 2 kg.
Replace ${a_1} = 2m{s^{ - 2}}$ in the relation\[{a_1} = 2{a_2}\],
\[
  {a_1} = 2{a_2} \\
  2 = 2{a_2} \\
  {a_2} = 1m{s^{ - 2}} \\
 \]
The acceleration of the ball of mass 2 kg is $1m{s^{ - 2}}$. Therefore, option (B) is the correct answer.

Note:
In the above question students should remember that the force applied by the spring on the body of mass 1 kg is $F = - k \cdot x$ and which is equal to the force applied by the spring on the body of mass 2 kg. Also, students should remember that the force applied on a body of mass m and acceleration a is given by $F = m \cdot a$, where $m$ is the mass of the body and a be the acceleration of the body.