Question

Two angles of a polygon are right angles and the remaining angles are $120{}^\circ $each. Find the number of sides in it.

(a) 5
(b) 4
(c) 3
(d) 2

Answer 1

Hint:This question is based on the sum of the internal angles of a polygon. First of all, we assume that the number of sides is $n$. Now by using the formula of the sum of internal angles of a polygon –
Sum of internal angles of $n$sided polygon $=\left( n-2 \right)\times 180{}^\circ $
By given angles in the question, we make an equation in $n$ and solve it and get the number of sides of a polygon.

Complete step by step answer:
Let us start by understanding what a polygon is. A polygon is a plane figure that is described by a finite number of straight-line segments called edges. There are an equal number of edges and angles in a polygon, and the sum of interior angles and side’s relation is –
$S=\left( n-2 \right)\pi $ radian
$S=\left( n-2 \right)\times 180{}^\circ $ degree
Let us assume that there are $n$ sides in a polygon. Thus, there are also $n$ internal angles in the polygon.
According to the question, we have the data as below.
Out of$n$, two angles are right angle. And the remaining $\left( n-2 \right)$ angles are $120{}^\circ $each.
So, we can write that
Sum of internal angles of polygon $=\left( 2\times 90{}^\circ \right)+\left( n-2 \right)120{}^\circ $ …(1)
As we know that sum of interior angles of $n$ sided polygon
$=\left( n-2 \right)\times 180{}^\circ $ …(2)
Now, by equation (1) and (2), we can equate them as
$\left( n-2 \right)\times 180{}^\circ =\left( 2\times 90{}^\circ \right)+\left( n-2 \right)120{}^\circ $
On dividing by $60{}^\circ $on both sides, we get
 \[\Rightarrow \left( n-2 \right)\times \dfrac{180{}^\circ }{60}=\dfrac{\left( 2\times 90{}^\circ \right)}{60}+\left( n-2 \right)\dfrac{120{}^\circ }{60}\]
$\Rightarrow 3\left( n-2 \right)=3+2\left( n-2 \right)$
By subtracting $2\left( n-2 \right)$ on both sides, we get
$\Rightarrow 3\left( n-2 \right)-2\left( n-2 \right)=3+2\left( n-2 \right)-2\left( n-2 \right)$
$\Rightarrow \left( n-2 \right)=3$
By adding $2$ on both sides, we get
$\Rightarrow n-2+2=3+2$
$\Rightarrow n=5$

Hence, the number of sides in the polygon is 5. Thus, the correct option is (a).
A diagram of a pentagon ABCDE with two right angles and three angles each of $120{}^\circ $ is shown below.

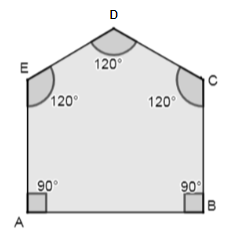
Note:
 In this type of question, students should take care of the angles given in degree or radian. Otherwise, they can make mistakes. Also, students should take care of calculations in solving equations. A silly mistake in the calculation can change the answer, and the whole question will be wrong. Most common mistake is that students might write the formula $S=\left( n-2 \right)\times 180{}^\circ $ as $S=\left( n-2 \right)\times 90{}^\circ $ and go wrong.