Question

Two adjacent sides of parallelogram are $ 24\;cm $ and $ 18\;cm. $ If the distance between the longer sides is $ 12cm, $ find the distance between the shorter sides.

Answer 1

Hint: A parallelogram is the simple quadrilateral with its two opposite sides parallel to each other. The opposite sides of the parallelogram are of same length and never intersect each other. Here we will draw a diagram with the given specifications and will use the formula of the area of the parallelogram to find the unknown side.

Complete step-by-step answer:
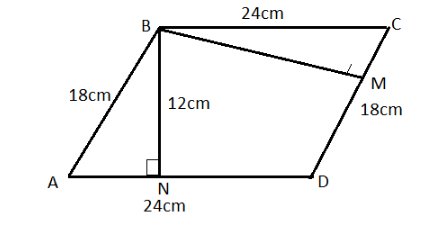
Given that ABCD is the parallelogram.
 $ AB = 18\;cm $ and $ BC = 24\;cm. $
Draw the diagram using the given conditions - $ \overline {BM} \bot \overline {CD} $ and $ \overline {BN} \bot \overline {AD.} $

As we know that the formula of the area of the parallelogram can be given by –
Area $ = $ Base $ \times $ perpendicular height
Now, in the parallelogram ABCD, given that $ AD = 24\;cm $ and perpendicular distance, $ BN = 12\;cm $
 $ \therefore A = AD \times BN $
Place the values in the above equations –
 $ \therefore A = 24 \times 12 $
Simplify the above equation –
 $ \therefore A = 288\;c{m^2} $ ..... (i)
Now, similarly for the area of the parallelogram using other perpendicular height-
Where, CD is the side of the parallelogram and the perpendicular height BM.
 $ \therefore A = CD \times BM $
Since the area remains the same in the same parallelogram, place the value from the equation (i) and the other value in the given data.
 $ \therefore 288 = 18 \times BM $
Make the required measure the subject and take other terms on one side. Remember when the term in multiplicative at one side is moved to the other side it goes to the denominator.
 $ \Rightarrow BM = \dfrac{{288}}{{18}} $
Do division –
 $ \Rightarrow BM = 16\;cm $ is the required answer.
So, the correct answer is “ $ 16\;cm$”.

Note: Follow the properties of the parallelogram properly. Always remember that the opposite two sides of the parallelogram are always equal. Be good in multiples and simplification for the accurate and an efficient solution.
Additional Information: Quadrilateral is the closed figure with four sides and the four vertices. It is also known as “quadrangle”. Basically, there are six types of quadrilaterals such as rectangle, square, kite, rhombus, trapezium and parallelogram. Refer the properties and know the difference among them.