Question

Two adjacent angles of a parallelogram are${\left( {3x - 4} \right)^ \circ }$ and ${\left( {3x + 10} \right)^ \circ }$ .Find the angles of the parallelogram.

Answer 1

Hint: Start by drawing a parallelogram and labelling the sides , consider any two adjacent sides as the given value. Apply the adjacent angle sum property of parallelogram to find the value of x , use alternate opposite angle property to find the other angles of parallelogram.

Complete step-by-step answer:

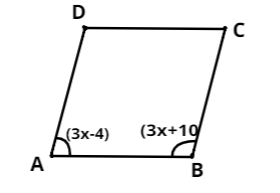
As we can see from figure parallelogram ABCD
Let A and B be the two given adjacent angles,
$\angle A = {\left( {3x - 4} \right)^ \circ }$ and \[\angle B = {\left( {3x + 10} \right)^ \circ }\]
Now, we know that the sum of adjacent angles of parallelogram are ${180^ \circ }$ .
We can write like this
$\angle A + \angle B = {180^ \circ } \to eqn.1$
Now , let us substitute the value of angles in equation 1, we get
$ \Rightarrow \left( {3x - 4} \right) + \left( {3x + 10} \right) = {180^ \circ }$
$ \Rightarrow 6x + 6 = {180^ \circ }$
Dividing by 6 on both the sides , we get
$ \Rightarrow x + 1 = {30^ \circ }$
$ \Rightarrow x = {29^ \circ }$
Now, putting $x = {29^ \circ }$ to find $\angle A$ and $\angle B$
$\angle A = {\left( {3 \times 29 - 4} \right)^ \circ }$ and $\angle B = {\left( {3 \times 29 + 10} \right)^ \circ }$
$ \Rightarrow \angle A = {83^ \circ }$ and $\angle B = {97^ \circ }$
As we know the opposite angles of parallelogram are equal
$\angle A = \angle C$ and $\angle B = \angle D$
$ \Rightarrow \angle C = {83^ \circ }$ and $\angle D = {97^ \circ }$
All angles of parallelogram A,B,C,D are ${83^ \circ },{97^ \circ },{83^ \circ },{97^ \circ } $respectively.

Note: Similar questions can be asked with different levels of intricacy with different shapes and can be solved using the above procedure. Students must know all the properties of parallelogram and triangles and other geometrical shapes in order to make and solve problems easier.