Question

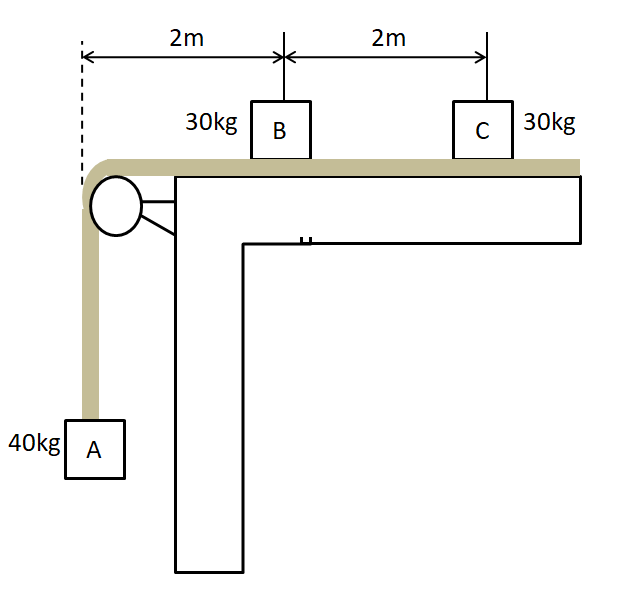
Two $30kg$ blocks rest on a massless belt which passes over a fixed pulley and is attached to a $40kg$ block. The coefficient of friction between the belt and the table as well as between the belt and the block B and block C is $\mu $. The system is released from rest from the position shown, the speed with which the block B falls off the belt is

A.$2\sqrt 2 m/s$ if $\mu = 0.2$
B.$2m/s$ if $\mu = 0.2$
C.$2\sqrt 5 m/s$ if $\mu = 0.5$
D.$2.5m/s$ if $\mu = 0.5$

Answer 1

Hint: To solve this question, we have to find out the direction and magnitude of the frictional force acting on the block B. From that, using the Newton’s second law of motion, we can find out the value of the acceleration, which can be substituted in the third equation of motion to get the final answer.

Complete answer:
As we can see in the figure given above, the block B is resting on the surface of the belt. Therefore, the only force which can start the motion of the block is the force of friction between the block and the belt. According to the question, the block is falling off the belt. So the maximum value of this frictional force must be acting on the block.
Also, from the figure, due to the block A attached to the massless belt, the belt will move forward. So relative to the belt, the block has a tendency to move backwards. We know that the force of friction opposes the relative motion between two surfaces in contact. So the frictional force will act in the forward direction on the block B, to oppose the relative motion. Therefore, from the free body diagram of the block B, we have

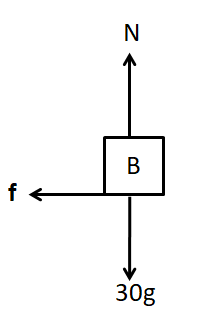
As there is no motion of the block in the vertical direction, so we have
$N - 30g = 0$
$ \Rightarrow N = 30g$ (1)
Also, in the horizontal direction, there is only frictional force acting towards the left. So the acceleration of the block will be towards the left. From the Newton’s second law of motion we have
$f = ma$
The mass of the block is given to be $m = 30kg$. Therefore we have
$f = 30a$ (2)
We know that the frictional force is given by
$f = \mu N$
From (1)
$f = 30\mu g$ (3)
Equating (2) and (3) we get
$30a = 30\mu g$
Cancelling $30$ from both the sides, we finally get
$a = \mu g$ (4)
So the acceleration of the block is constant and is equal to $\mu g$.
From the figure given in the question, the block has to cover a displacement of $2m$ before falling off the belt. So the displacement of the block is
$s = 2m$ (5)
From the third kinematic equation of motion, we have
${v^2} - {u^2} = 2as$
As the system is released from rest, so we substitute $u = 0$ above to get
${v^2} = 2as$
Taking square root both sides, we get
$v = \sqrt {2as} $
Substituting (4) and (5)
$v = \sqrt {4\mu g} $
$ \Rightarrow v = 2\sqrt {\mu g} $ (6)
Now, in the options, we have two values of coefficient of friction, one is $0.2$ and the other is $0.5$.
Substituting $\mu = 0.2$ in (6) we get
$v = 2\sqrt {0.2g} $
We know that $g = 10m/{s^2}$. So we get
$v = 2\sqrt {0.2 \times 10} $
\[ \Rightarrow v = 2\sqrt 2 m/s\]
So the speed of the block is \[2\sqrt 2 m/s\] if $\mu = 0.2$.
Now, substituting $\mu = 0.5$ in (6) we get
$v = 2\sqrt {0.5g} $
Substituting $g = 10m/{s^2}$, we get
$v = 2\sqrt 5 m/s$
So the speed of the block is $2\sqrt 5 m/s$ if $\mu = 0.5$.

Hence, the correct options are A and C.

Note:
The above question appears to be very difficult when we look at it at first sight. But when we carefully read the question, we have already been given that the block is sliding over the pulley, so that acceleration of the block is constant and we do not need to carry any other analysis.