Question

Triangles ABC and DBC are on the same base BC with A and D on opposite sides of line BC such that area $\left( \Delta ABC \right)=$ area $\left( \Delta DBC \right)$. Show that BC bisects AD.

Answer 1

Hint: To prove that the side BC bisects AD, draw an appropriate figure that corresponds to the given data. Then prove that the two triangles have equal heights. Later, you can use congruence rules to prove the given statement.
Formula used:
$area(\Delta )=\dfrac{1}{2}\times base\times height$

Complete step-by-step answer:
The first thing to do in this type of question is to draw an appropriate figure with the help of the given data.
It is given that triangles ABC and DBC are on the same base BC and the vertices A and D are on the opposite sides of the side BC.
First, draw the line segment BC. Then taking BC as the common base, draw the two triangles up and down as shown.

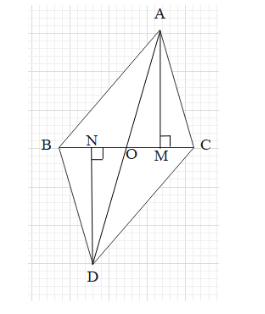
The area of a triangle is equal to half of the product of its base and its height.
i.e. $area(\Delta )=\dfrac{1}{2}\times base\times height$.
Let the height of $\Delta ABC$ be AM and the height of $\Delta DBC$ be DN.
Therefore,
Area of $\left( \Delta ABC \right)=\dfrac{1}{2}\times BC\times AM$ … (i) and
Area of $\left( \Delta DBC \right)=\dfrac{1}{2}\times BC\times DN$ …. (ii)
But, we know that the area of $\left( \Delta ABC \right)=$ area of $\left( \Delta DBC \right)$.
Therefore, equate (i) and (ii).
$\Rightarrow \dfrac{1}{2}\times BC\times AM=\dfrac{1}{2}\times BC\times DN$
$\Rightarrow AM=DN$ …. (iii)..
Now consider $\Delta AMO$ and $\Delta DNO$.
Here, we just now proved that $AM=DN$.
Since height is perpendicular to the base, $\angle AMO=\angle DNO={{90}^{\circ }}$.
The angles AOM and DON are vertically opposite angles. This means that $\angle AOM=\angle DON$
Therefore,
$\Delta AMO\cong \Delta DNO$ by AAS congruence rule.
Now, since $\Delta AMO\cong \Delta DNO$, $AO=DO$.
But $AO+DO=AD$.
$\Rightarrow AO=DO=\dfrac{1}{2}AD$
This means that the side BC bisects AD.
Hence proved.

Note: In this question, we see that the two triangles having same base and equal area have equal heights. Hence, we proved another theorem that two triangles with the same base and equal area have equal heights.
This theorem is applicable even when the two triangles have equal bases but not common.