Question

How do you translate the graph of $ y = \sin x - 2 $ ?

Answer 1

Hint: In order to graph the above trigonometric function, first draw the graph of the sine function. Use the fact that there is a number in the end of sine function, then there will always be a Vertical shift. If the number is positive, then Vertical Shift Up Else Vertical Shift Down. In our case the number is $ - 2 $ so there is Vertical Shift down two units.

Complete step-by-step answer:
We are given a trigonometric function i.e. $ y = \sin x - 2 $
Recall that the domain of sine function is in the interval $ \left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right] $ and the range of the same is in the interval $ \left[ { - 1,1} \right] $ .
Lets first draw the graph of sine function $ y = \sin x $

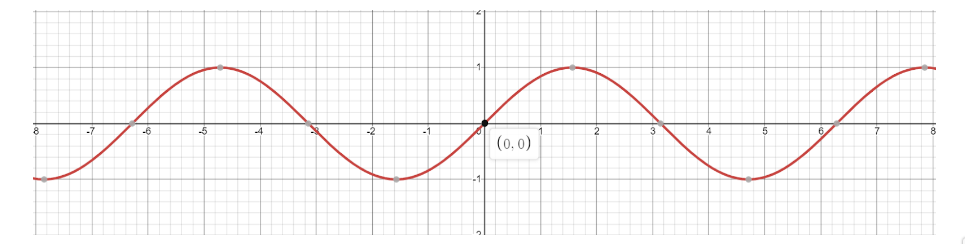
If you add any number on the end of the sine function, then there will always be a vertical shift of the graph. When the number is positive then there will be a vertical Shift up and if the number is negative then Vertical shift down.
In our case, the number is negative i.e. $ 2 $ so the graph will have a Vertical Shift down two units, which gives the following graph :

Hence, we’ve successfully plotted our graph of equation $ y = \sin x - 2 $

Note: 1.Draw the cartesian plane only with the help of straight ruler and pencil to get the perfect and accurate results.
2.Mark the points carefully.
3. x-intercept is the point at which the line intersects the x-axis of the plane and similarly y-intercept is the point at which line intersects the y-axis of the plane.
4. Before solving such types of problems , first check whether there is a vertical shift or horizontal shift. Horizontal shift is when some value is added or subtracted from the $ x $ variable. For example $ y = \sin \left( {x \pm c} \right) $ .If it is negative then there will be a right horizontal shift and when it is positive then left-horizontal shift .