Question

TP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P’ and Q’; Prove that:
$\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1$

Answer 1

Hint: Use parametric form of representation for representing the coordinates of a point on the parabola, ${{y}^{2}}=4ax$ (Standard equation of a parabola). Write the coordinates of P, Q and R in parametric form, since according to question P, Q and R lies on the parabola.
Now, use the section formula to get the ratios $\dfrac{TP'}{TP}and\dfrac{TQ'}{TQ}$ and then add them to get the result.

Complete step-by-step answer:

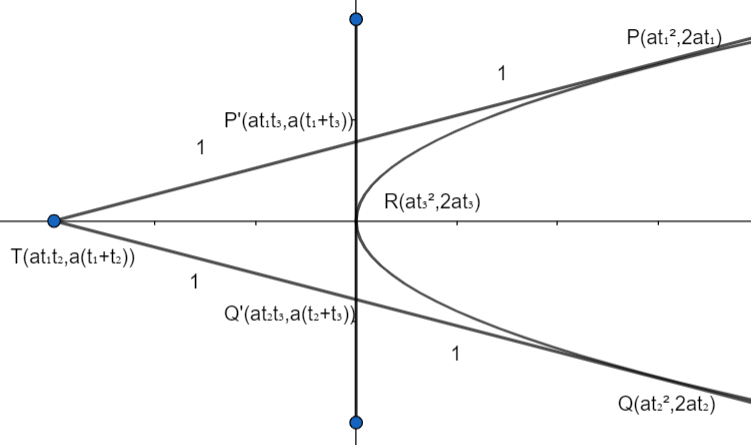
The parametric representation of the coordinates of a point on the parabola${{y}^{2}}=4ax$ is $\left( a{{t}^{2}},2at \right)$.
According to the question, point P, Q and R lies on the parabola.
TP is the tangent at point P.
TQ is the tangent at point Q.
P’Q’ is the tangent at point R.
We know that if tangent to the parabola ${{y}^{2}}=4ax$ cuts at point $\left( a{{t}^{2}},2at \right)$, then equation tangent is given by $ty=x+a{{t}^{2}}$
Let, coordinates of P be $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$
So, equation of tangent on parabola at point P will be ${{t}_{1}}y=x+a{{t}_{1}}^{2}$
Coordinates of Q be $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$
So, equation of tangent on parabola at point Q will be ${{t}_{2}}y=x+a{{t}_{2}}^{2}$
Coordinates of R be $\left( a{{t}_{3}}^{2},2a{{t}_{3}} \right)$
So, equation of tangent on parabola at point R will be ${{t}_{3}}y=x+a{{t}_{3}}^{2}$
Since, point of intersection of the tangents at the point ${{t}_{1}}\ and\ {{t}_{2}}\ is\text{ }T\ \left[ a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right]$.
Similarly, point of intersection of the tangents at the point ${{t}_{2}}\ and\ {{t}_{3}}\ isQ'\ \left[ a{{t}_{2}}{{t}_{3}},a\left( {{t}_{2}}+{{t}_{3}} \right) \right]$.
Similarly, point of intersection of the tangents at the point ${{t}_{1}}\ and\ {{t}_{3}}\ isP'\ \left[ a{{t}_{1}}{{t}_{3}},a\left( {{t}_{1}}+{{t}_{3}} \right) \right]$.
Hence, coordinates of $T=\left[ a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right]$
Coordinates of $P'=\left[ a{{t}_{3}}{{t}_{1}},a\left( {{t}_{3}}+{{t}_{1}} \right) \right]$
Coordinates of $Q'=\left[ a{{t}_{3}}{{t}_{2}},a\left( {{t}_{3}}+{{t}_{2}} \right) \right]$
Section formula: The coordinates of a point dividing a line joining the points $A\left( {{x}_{1}},{{y}_{1}} \right)\ and\ B\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio m:n is given by,
$\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$
Let, the ratio constant be $\lambda $ ,
i.e.
$\begin{align}
  & \dfrac{TP'}{TP}=\dfrac{\lambda }{1}............\left( 1 \right)=\dfrac{TQ'}{TQ} \\
 & Now,\ \lambda =\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{2}}}=\dfrac{TP'}{TP}.......\left( 1 \right) \\
\end{align}$
(Using section formula, as $TP':TP=\lambda :1$ )
Hence,
$\begin{align}
  & P'\left\{ a{{t}_{1}}{{t}_{3}},a\left( {{t}_{1}}+{{t}_{3}} \right) \right\}=\dfrac{\lambda \left( P \right)+1\left( T \right)}{\lambda +1} \\
 & Similarly, \\
 & \dfrac{TQ'}{TQ}=\dfrac{{{t}_{1}}-{{t}_{3}}}{{{t}_{1}}-{{t}_{2}}}.............\left( 2 \right)\left\{ \begin{matrix}
   \text{since},TQ':TQ=\lambda :1 \\
   Q'a{{t}_{3}}{{t}_{2}},a\left( {{t}_{2}}+{{t}_{3}} \right) \\
   =\dfrac{\lambda \left( Q \right)+1\left( T \right)}{\lambda +1} \\
\end{matrix} \right. \\
\end{align}$
Now, Adding equation (1) and (2), we get,
\[\begin{align}
  & \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{2}}}+\dfrac{{{t}_{1}}-{{t}_{3}}}{{{t}_{1}}-{{t}_{2}}} \\
 & \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{{{t}_{3}}-{{t}_{2}}+{{t}_{1}}-{{t}_{3}}}{{{t}_{1}}-{{t}_{2}}} \\
 & \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{{{t}_{1}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{2}}} \\
 & \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1 \\
\end{align}\]

Note: Students can make mistakes here by finding the distance TP, TP’, TQ and TQ’ using distance formula after writing coordinates of points P, Q, P’, Q’ and T using parametric form. But students need to find the ratio $\dfrac{TP'}{TP}and\dfrac{TQ'}{TQ}$. Hence, they need to find this ratio using the section formula, by taking the (assuming) ratio constant $\lambda $.