Question

Towns $A$ and $B$ are $16$ miles apart. How many points are $10$ miles from town $A$ and $12$ miles from town $B$?

Answer 1

Hint: Here in this question we have been asked to find the number of points which are 10 miles away from town “A” and 12 miles away from town “B” when town “A” and “B” are 16 miles apart. For that case we will assume a circular fence around town “A” and “B” individually with radius 10 and 12 miles respectively.

Complete step-by-step solution:
Now considering from the question we have been asked to find the number of points which are 10 miles away from town “A” and 12 miles away from town “B” when town “A” and “B” are 16 miles apart.
For that case we will assume a circular fence around town “A” and “B” individually with radius 10 and 12 miles respectively.

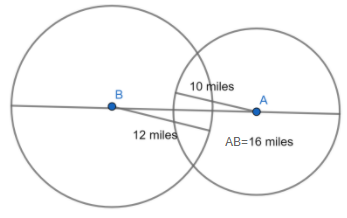
Now we can say that all the points lying on the fence of town “A” are 10 miles away and similarly for the case of town “B”.
Now if we consider the concept of intersection of two circles. We know that when the sum of the radius is greater than the distance between the circles then we have two points of intersection.
Similarly here also we have two points of intersection.
Therefore we can conclude that there are two points which are $10$ miles from town $A$ and $12$ miles from town $B$ when both the towns are 16 miles apart.

Note: During this process we should be clear with the concepts that we apply. Similarly we have two more cases in the concept of intersection of two circles given as
(i) When the sum of the radius is equal to the distance between the circles then we have one point of intersection.
(ii) When the sum of the radius is less than the distance between the circles then we have no points of intersection.